
最初に、南極点、あるいは北極点に立ってることを考えよう。
「…死ぬほど寒いよ。あ、白熊とシャチが盆踊りを…」
そういう余計な事は考えなくていい。
とりあえず、極点から周辺部に砲撃する場合を見てみるぞ。
北極点でも南極点でもどっちでもいい。
極点上に大砲を設置し25km先の目標を狙うとする。
この時、目標は地上に固定されているとする。
よって、難しい計算はいらないね。
方角さえ測ったら、後は距離25kmとわかってるんだから、
そこを狙ってガンガンに撃つだけだ。
「なんでわざわざ極点なのさ?自転速度が0というのがポイント?」
なかなかするどいね。
その通りだ。その条件だと説明が手っ取り早いんだよ。
さて、砲撃の正確性を期するため、人類最高の砲撃手が撃つとして、
この時、砲弾は目標に当たるだろうか。図にするとこうだ。
「…図にしない方がよくないか、なんか、全体的に…。
そもそも、砲撃手にそれだけの技量があるなら当たるだろ。
照準による誤差も発生しないんでしょ」
が、当たらないんだよ、これが。
「そんなわけあるかい」
あるんだ。それが地球の自転の仕業なのさ。
ここで重要な点は二つ。
1、主砲の砲弾は一度撃ちだされたら、その方向にひたすら直進する。
2、極点は速度0だが、その周辺は地球の自転で動いてる。
「だから?」
こうなるのさ。
「なんかハラの立つ図だな…
で、…え?地球の自転で目標が動くって、つまりどういうこと?」
時速0の極点から打ち出された砲弾はひたすら直進してゆく。
で、25km先の敵に当たるには、約45秒程度かかるわけだ。
「それは前にも聞いたよ」
だがこの時、極点から25kmはなれた場所は、
極点を中心に自転、つまり円運動をしてる。
半径25kmの円周それを24時間で割れば時速になるから、
時速約6.5km、分速で約109.1m、秒速なら約1.8mで絶賛円運動中だ。
「…だから?」
つまり、砲弾が到着する45秒後には約81mも移動してしまうのさ。
「そうなの?ええー?でも人が歩くのより速い速度で
地上の目標が動いていくなんて、想像できないぞ」
それは正しい。実は同じ地表、あるいは地表付近にいる限り、
目標の移動を認識することは人間には不可能なんだ。
この理屈はまた面倒なので、今回はパス。
とりあえず、その結果、こんな感じに見えることになる。
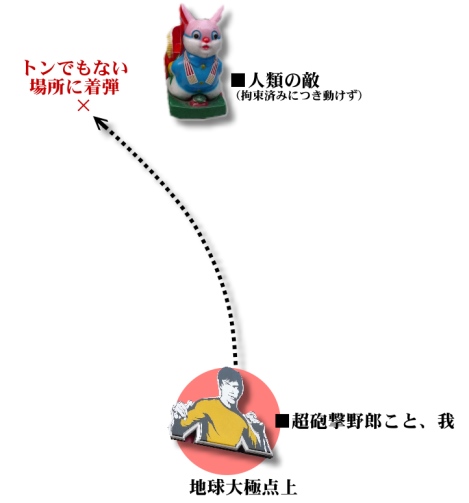
「砲弾の方が曲がる?」
そうなんだ、地上の人間が見ると、砲弾の方が目標から逸れたように見える。
「実際は直進してるのに、何かの力が働いたように見える」
いわゆる「見かけ上の力」だね。これがコリオリの力だ。
長距離砲撃には、こういった影響があるんだよ。
この時、どちらに曲がる(ように見える)かは地球の自転方向次第で、
南半球と北半球では逆になる。
えー、とこの図だと左に曲がってるから、多分ここは南極点だね。
「またキチンと考えないで適当に描いたな…」
NEXT