
というわけだ、ペロ君。
「というわけだって、さっぱりわかんねえよ、あれじゃ」
ではもう少し、具体的にどんな現象なのか、を見てみよう。
ちなみに以下の図はGIFアニメだから、ブラウザはGIFアニメを見れる設定してね。
でないと、えらく苦労したのが悲しくなるから…
なんか矢印がヘロヘロ動いていれば大丈夫。
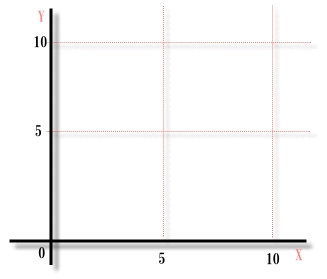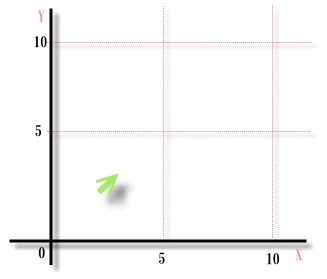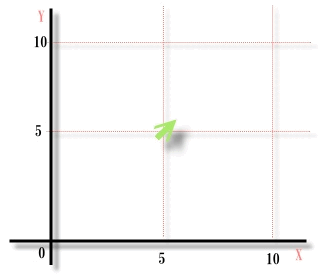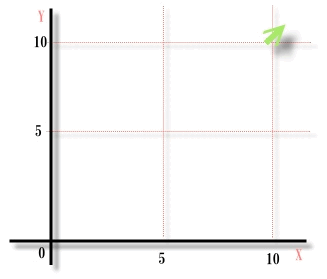
「なんだこりゃ」
全く動いてない平面を矢印が移動してるとこだね。
「いや、だからそれに何の意味が…」
とりあえず、これが普通の状態、と思ってちょうだい。
で、この運動は矢印の位置を(X1、Y1)、(X2、Y2)、
と示すことが可能だ。見ての通り、一直線の等速運動だから数式も
Y=1X
といった、極めてシンプルなものになる。
で、次に平面が回転運動してる状態での矢印の移動を見てみよう。
「これがどうしたの?」
二つある座標軸に対する、矢印の取るそれぞれの座標に注目しよう。
まず、一緒に回転してる座標軸の中では、上で書いた単純な式が常に成立している。
矢印と座標軸は一緒に動いてるんだから、その位置関係に変化はないんだ、
当然といえば当然。
が、薄く見えてる下の座標、動いてない座標から見た場合、
矢印は単純な直線運動をしてるような軌道を示さない。
動かない座標軸に対して、矢印がY=1Xといった単純な運動をしてないのはわかるだろ。
「うーん、なんとなく。結局どうなってるわけ?」
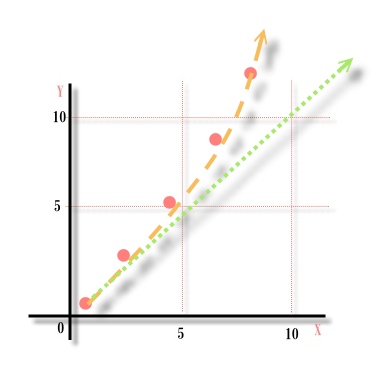
こうなってる。
緑の矢印が回転してる座標内での矢印の動き、
オレンジが、それを固定された座標から見た場合の動き。
「曲がってる?」
そう、これがコリオリの力、だ。
実際は矢印は動かない方の座標に置いて考えるんだけど、
GIFアニメを造る時、間違えちゃった、テヘ。
まあ、この方がわかりやすいでしょ。
「どうだかねえ…」
これが地球上でおこるわけさ。
自転してる地球上を直進しても、地球上から見たら、
それは曲がっている軌道に見える。
実際、曲がったとしか思えない場所に着弾するしね。
これが回転系の運動で見られる現象なわけだ。
「うーん、わかったような、わからないような」
NEXT