
さて、というわけで、一斉にぶっ放した砲弾がどうやって着弾するか、を考えよう。
そのバラつきは、一般に縦長の楕円の範囲に広がる。これを砲弾の「散布界」と呼ぶんだ。
奥行き方向、弾を撃ち込んだ方向に縦長になるのが普通。
さて、ここで考えてみよう。下の線で囲んだ範囲内に着弾した二つのケースがあったとする。
AとB、どちらの方がより大きな命中率を期待できると思う?
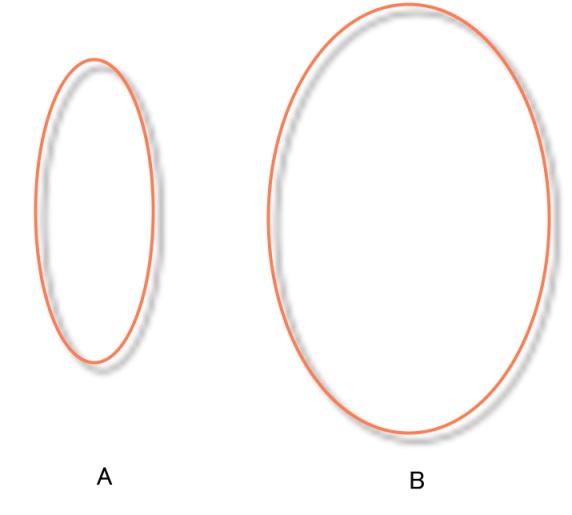
「Aなんじゃないの。弾着が近距離に密集してるんだから、それだけ命中しやすいだろ」
と、いうのが、理想論。
だが、それは目標と着弾散布界の真ん中、
いわゆる射撃中心(以下“射心”)が大きく外れてない場合のみの話だ。
つまり、キチンと目標に弾が向かっていったケースでのみ正しい。
もし射撃がヘタレで着弾が目標から大きくずれてしまった場合、
右の範囲の広いほうがむしろ当たる可能性がある。
「そうかあ?」
確率的にはかなり低いんだけどね。理屈の上ではそうなるんだ。
例えば上の図でA,Bの文字のちょっと上の位置に敵艦がいた場合、
Aの散布界ではその命中可能性は0だが、Bでは0ではない。
数字の上で0と0でない、というのは全く別次元と言うくらい差がつくんだよ。
ちなみに、こんな感じだ

「なにこれ?変な戦艦の写真だな?」
模型ショーの時撮影したハセガワのキットのパーツだからね。
確か金剛だったかな。まあ気にするな。あくまで大きさの参考だと思って欲しい。
という感じで、どちらが有利とは単純には言い切れないんだ。
ペロ君の考え方も、全くもって正しいのだが、前提条件がいる、ということになる。
つまり“きちんと敵艦に向けてちゃんと弾が飛んでゆく場合”ならAが正解。
これは砲撃が正確、というだけでなく、当然、その前の照準の正確さが要求される。
それ以外の場合は、実は何ともいえない、が正解。
「まあでも、ちゃんと狙った場所に弾が飛んで行けばAの方が当たりが出やすいんだろ」
その通り。まあ、直感的に理解できる話だが、今後のため、キチンと確認しよう。
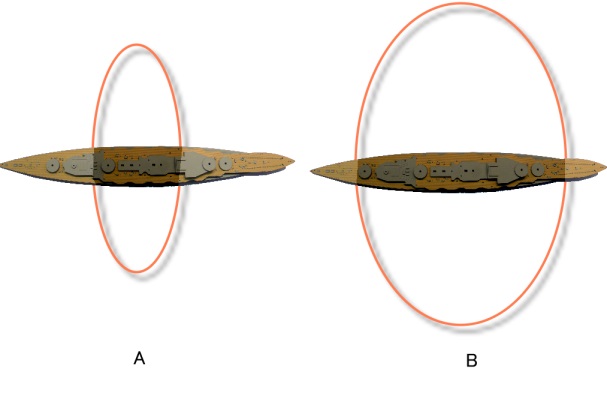
色が濃くなってるのが砲弾の当たる可能性を持つ部分となる。
「あれ?でもBの方が命中の可能性を持つ部分の面積が広くない?」
広い。
でも、この場合、それぞれの楕円形内で占める面積の方が問題になるんだ。
例えば、足元に30cm四方の正方形を書いたとしよう。
この1/2を黒く塗った場合と、1/4を黒く塗った場合、
適当に上から石を落として、黒い部分に入る可能性はどっちが高い?
「そりゃ1/2の方だろう」
豊後。否、ビンゴ。
だから、楕円内で船体がより大きな面積を占めている方が砲弾の命中率は高い。
これは明らかにAだよね。
よって“きちんと目標に向かって砲弾が送り込まれている限りにおいては”
着弾の散布界は小さいほうが望ましい、となる。
NEXT