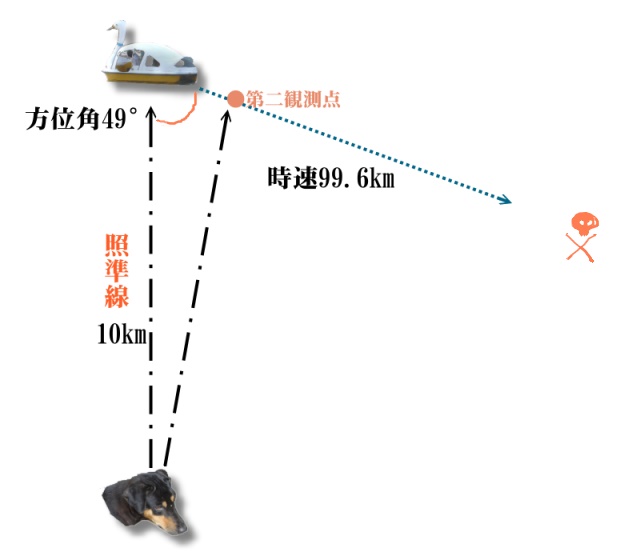
と、いうわけで、現在、我々の持っているデータがこれです、サー。
さあ、ここからいよいよ、魚雷の発射速度と射角を決定しますよ。
とりあえず、命中ポイントを決めて、そこにドカンと打ち込みます、サー。
「ぐー…」
…気持ちはわかりますが、もう一息だからがんばってください、サー。
「…はい、はい、えーと、後はどうすりゃいいんだっけ?」
とりあえず、目標艦の5分後の位置を出してみましょう。
分速1.66kmですから、5分後には8.3km先まで進みます。
第二観測点までの段階で、すでに1.66km進んでましたから、
照準線から9.96kmほど前進した位置に、方位角49度で到達します、サー。
つまりこのような状態です。
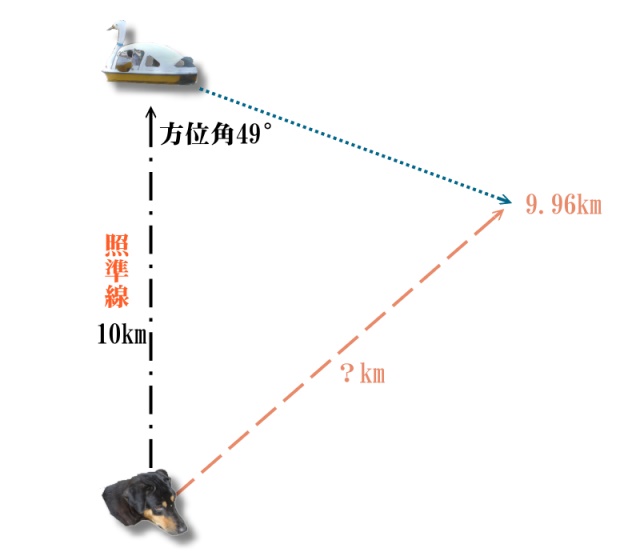
「ああ!これならなんとかなりそうジャン!」
もちろん、なるんですよ、サー。
?の距離を求めて、それを5分で走りきる速度が魚雷の設定速度となります。
そして、?の距離が出たなら、当然、射角も三角関数で求められます。
ちなみに今回は方位角を∠Aにして、最初の余弦定理に当てはめるだけです。

はい、さくさく行きましょう、答えは約8.28km。もう後は簡単ですね、サー。
魚雷はこの距離を5分で走ればいい。
8.28kmを5分で割れば、魚雷の設定速度が決まります。
分速1.66km、時速99.4km。
目標艦とほぼ同じような速度になりましたね。
最後の射角はこれまた、さっきの余弦定理の変形版、
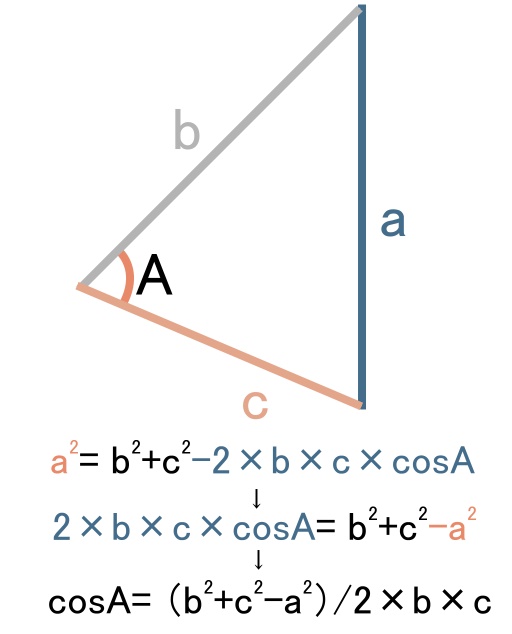
これを使ってcosを計算し、そこからアークタコサイン、arccosを求めます。
この時、∠Aにあたるのが射角で、辺aは目的艦の進行距離、9.96kmとなります。
で、もう答えだけ書いてしまえば、約49度。
作図が適当なんでそうは見えませんが(涙)、ほぼ二等辺三角形になります。
はい、ようやく射角がでました。49度。
そして魚雷の速度は99.4km。
いや、ようやくですね、サー。
ちなみに発射のタイミングは、この場合、今すぐ撃て、になります(笑)。
とりあえず、魚雷速度時速99.4km、射角49度で撃てば、
5分後には命中、となるわけです。
ようやく、これで魚雷の照準が終りました。
これを魚雷発射管の操作担当者に伝えて、この数字の通りに撃ってもらうわけです。
「いや、なるほど、大変だ。でも、やればできるもんだなあ」
いや、あんたは何もしてませんよ、サー。
NEXT