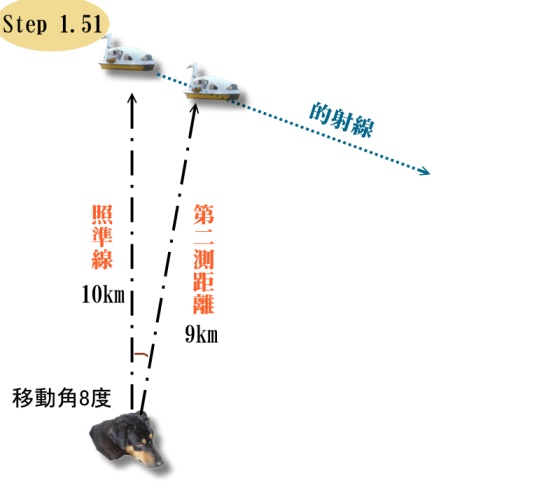
さあ、この状態で余弦定理を使ってみます。
∠A、移動角は8度ですから、cosA=約0.99、これを使って計算すると、
移動角に触れてない辺、すなわち目標の移動距離が出ます。
ちなみに普通に計算して出てくる数字はaを2乗した数字ですから、
最後に平方根を取るのを忘れないように。
私はこれでちょっとエライ目に会いました、サー…。
で、答えを書いてしまえば、約1.66kmです。
そして、これは1分間の移動距離でしたから、分速1.66kmという速度が出ます。
やりました、やりましたよ、サー!
つーか、適当に角度と距離の数字を決めたもんだから、
このスワンボート、時速99.6kmになっちゃいましたよ、ちきしょーめ(笑)!
「図、描きなおせば?」
絶対にいやです、サー。
連邦のスワンボートは化け物なんですよ、サー。
「まあいいけどさ…。でも、もう一つの要素、目標の方位角は?」
いいツッコミです、サー。
これがわからないと、速度だけでは目標の未来位置はわかりません。
で、せっかくここまで研究した、この三角形にもうひと活躍してもらいます。
ここまで来たら、一揆に行きますよ、サー。
「どこに行くんだよ。一気にだろ」
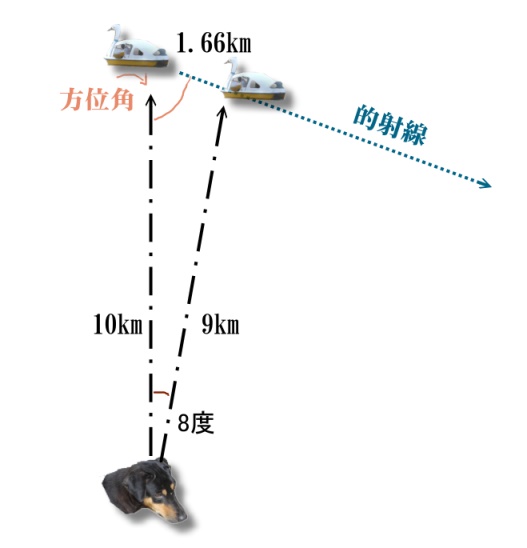
現状はここまでわかってます、サー。
で、方位角の角度が知りたいわけです。
「そうだけど、例の余弦定理って角度は計算できないでしょ?」
ところがドンスコイ、ちょっと式を変形させると、cosAを計算で出せます。
ちなみに今回の∠Aになってるのは方位角ですので注意を願います、サー。
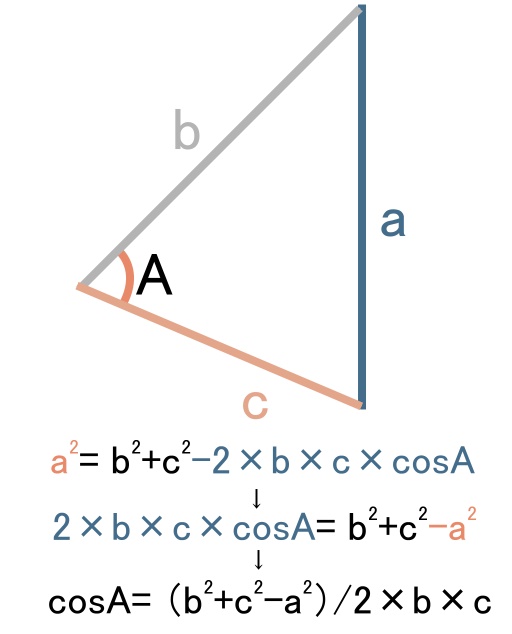
これで、∠A、今回は方位角にあたる角のcosの値が出ます。
ちなみに計算結果は約0.656となります、サー。
「…そのコサインとかがわかると、どうなるの?」
えー、実はここからが、ちょっと申し訳ないポイントです、サー。
cosから角度を求めるには逆三角関数を使う必要があるんですが、
これはちょっと説明しきれません。
「無責任だなあ…」
とりあえず、今回はcosの逆三角関数、arccosを使うだけで角度は出る、
とこう考えていただきたい、こう思う次第であります、サー。
「それだけでいいの?」
理屈は置いといて、計算だけなら、簡単にでます。
ついでにラジアンの話とかも忘れてくれると助かります(涙)。
で、答えだけ書いてしまえば、arccos0.656=約49度です、サー。
「あれ?じゃあ、これで?」
サー、イエッサー。
ついに我々はゴールにたどり着いたのであります。
目標の速度は時速99.6km、その方位角は49度、となります、サー。
「えらく大変だったねえ…」
つーか、あなたは何もしてませんが、サー。
まあ、最後は一気に数字がそろってしまうわけです。
さあ、この数字で、魚雷を照準しましょう!
NEXT