もうわかりましたね、サー。
「何が?」
いや、どうすればいいかですよ、サー。
とりあえず、速度を求めるために、目標艦の移動距離を出すんです。
「……」
……
「……@てへ?」
…余弦定理、余弦定理を使うんですよ、サー。
「え…よ…預言?…ごめん、どんな料理だっけ?」
…………
「…………」
…………オッケー!
ここは一つ、気を取り直して、パーっと行きましょう、パーっと!
ハハハハハ、ちきしょーめ、
こうなるんじゃないかと思ってましたよ、サー。
とりあえず三角関数のCOS(コサイン)を使います。
三角関数に関する解説は、ご容赦。
私でも問題なく理解できる理屈ですから、知らない人でも、
ちょっとネットで検索すれば問題なし!
そう決めた!今回はCOSしか使わないし!
では、ここで余弦定理を見てみましょう!イヤッハー!
みんなで呼ぼう!余弦定理さーん!
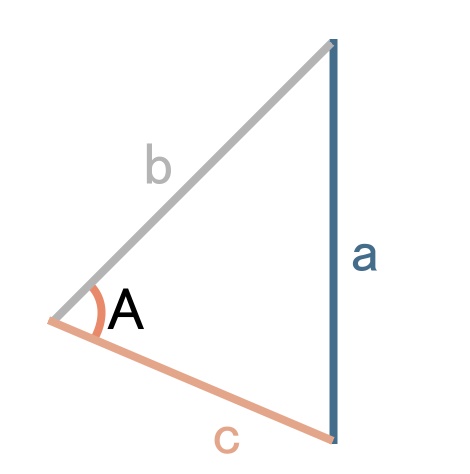
はーい、余弦定理でーす!
辺abcからなる三角形で、辺aと接してない角をAとします。
この時、以下の式が必ず成立するので、
三角形の2辺と一つの角度がわかれば、
残りの辺の長さを逆算で求めることが出来ます。

「長い式だなー、ややこしい」
いや、やってることは極めて単純ですよ、サー。
「…コサインとかさ、難しいこと言われても……
えー、bとcを2乗して……って、あれ?なんかこの式って…」
気が付かれましたか、サー。
「前半はこれと一緒じゃん」

見事です、見事ですよ、サー。
期待通りの展開です、今回はいい意味で。
そう、ピタゴラスの定理によく似てます。
「うははは、やっぱそうだよね」
で、sin(サイン)、cos(コサイン)、tan(タンジェント)は、
特定の角度には特定の値が決まってる、というのは覚えてますね、サー?
「………てへ」
オッケー、オッケーですよ、サー。
決まってるんです。
さあ、画面の上にスクロールしてしまったから、
余弦定理の図、もう一回、掲載しますよ。

実は、ピタゴラスの定理というのは、∠Aが90度、
直角のケースなんです、サー。
三角関数表を見るなり、表計算ソフト等で計算なりしてみると、
cos90度というのは0だ、という事がわかります。
上の式で、cosAに0を代入すると…。
はい、見事2×b×c×cosAが消えて、ピタゴラスの定理のみが残ります!
ジャジャーン、サー!
「あ、ホントだ!」
余弦定理、恐るに足りず!
たかがピタゴラスの定理に毛が生えて二本足歩行して、
地獄の盆踊りを踊れる程度のもんです!ざまーミロ!
「…ちょっと落ち着きなよ、ね」
…落ち着きました、サー。
まあ、余弦定理の特殊例がピタゴラスの定理なんですよ。
後半部分が隠されていたわけで。
なので、そんなに難しく考えなくても大丈夫。
ただし、計算そのものは計算機、できれば関数電卓、
表計算ソフトなどが無いと、しんどいですが…。
「そんな計算を第二次大戦時にやってたの?」
一応、専用のアナログ計算機が用意されてたほか、
前もって計算して、早見表のようなものを作成してたようです、サー。
「たいへんだねえ…」
はい、当時としては大変な話なんですよ、サー。
とりあえず、本題にもどりましょう。
NEXT