と、いうわけです、サー。
「まあ、わかったような、わからんような…」
ページが変わったので、もう一度図を見てみます、サー。
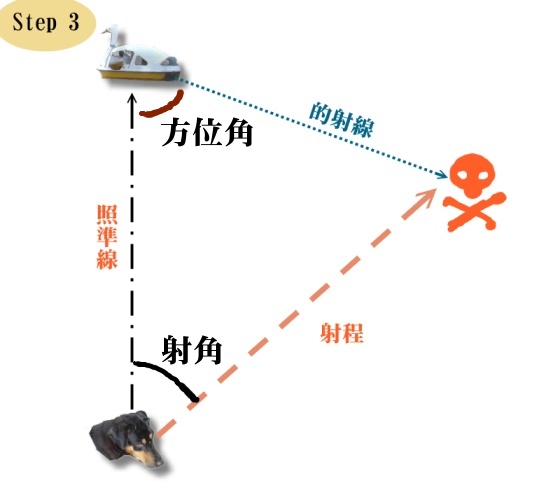
「結局、魚雷の発射に必要な射角を求めるには、魚雷の速度を決めなきゃだめ」
正解。
「そして、それを決めるには目標スワンボートの速度と進行方向を知る必要がある?」
エクセレント。その通りです、サー。
「で、今我々の手元にある情報はこれだけ、と」

その通りです、サー。
「絶望的に、どうしようもないんですけど…」
見える、と言うことはその精度はともかく、
測距儀で距離は測れる、という事ですよ、サー。
「距離って意味あるの?」
とりあえず照準線の測距をやってみましょう、サー。
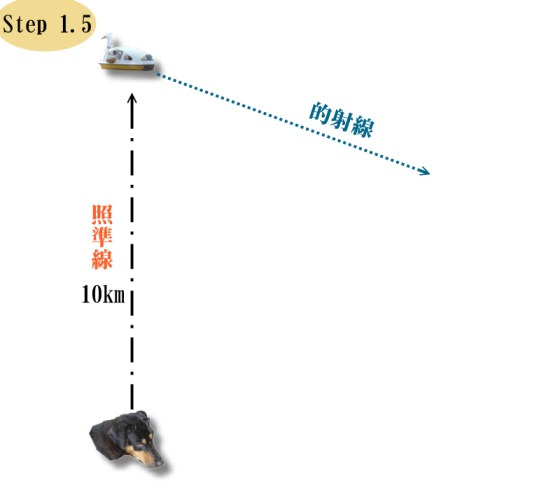
ほら。
「いや、ほらって言われてもなあ」
いいですか、速度と方向を求める、ということは、
例外なく、どこか二点で目標を測定する必要があります、サー。
「そうなの?」
相手がほぼ動いてない、ある一瞬の状態の観測では、
速度はもちろん、方向だってわかりませんよ、サー。
よって、照準線を決めた後、もう一度、
目標がある程度移動した状態で測定をやるのです。
「はあ」
さあ、1分たちましたから、もう一度、測定してみましょう。
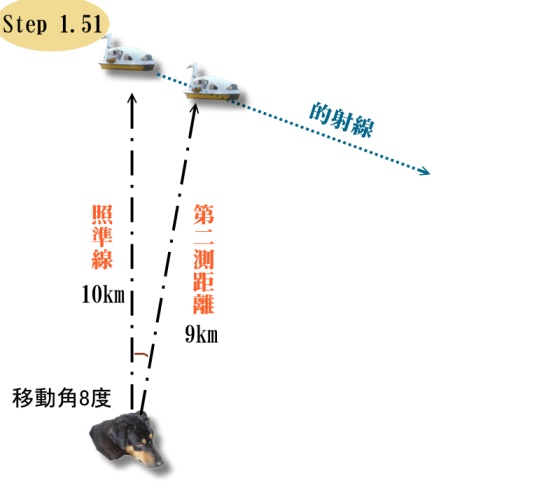
ほら、ほら。
「あ、なんか情報、増えたね」
そうです、サー。
2点で観測する事によってなんと2辺の長さと一つの角度が出ました。
さらに!プラス!
我々は、これが1分の時間が経過した状態だと知っています。
わが手には、距離、角度、そして時間までもが手に入ったのです、サー!
「あ、ハイ、ハイ!わかったよ、オレ、わかっちゃった!
1分で8度の角度分移動した、ということは次も1分後に8度移動してるから、
それを元に魚雷の発射角度を計算すればいいんだ!」
期待通りの展開です、サー。
きっとそう考えてくれると思っていました。
そしてそれは、目標艦が照準線の距離を半径とした
円運動をしてる時のみ正解なのです、サー。
「え?つまり?」
通常はありえない話です、サー。
また図に…して…みましょう…。
「…お疲れ様…」
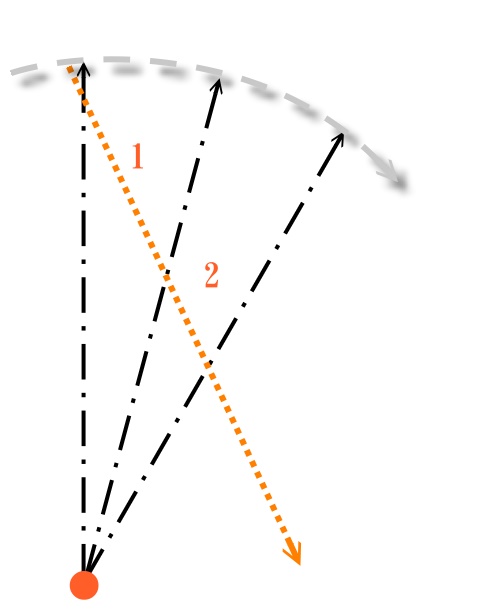
黒い点線が照準線の長さ。同じ角度差で3本描いてます。
この線端をトレースする軌道、つまり照準線を半径とした円の上を移動するなら、
移動距離は一定ですから、常に1分後の移動角は同じ、になります。
が、実際の動きとしては、オレンジ色の線のように移動するのが普通でしょう。
1と2の間の、オレンジ線の長さを見ると、その長さは異なります。
同じ時間の移動距離だったら、同じ長さになるはずですから、
1分後の移動角度は常に一定ではない、という事になります。
NEXT