應嫍媀偺婎杮揑側栤戣偼丄應掕偡傞嫍棧偑怢傃傞傎偳丄
傢偢偐側岆嵎偟偐嫋偝傟側偔側傞丄偲偄偆揰偱偡丅
椺偊偽1m偺婎慄挿偼抁偡偓傞丄
偲偄偆帠偱擔杮奀孯偺傛偆側10m偺應嫍媀傪梡堄偟偰傕丄
偦偺50攞偺500m偺嫍棧偱偡傜丄撉傒庢傝偵偼嬌傔偰彫偝側岆嵎偟偐嫋偝傟傑偣傫丅
偙偺応崌丄撉傒庢傞昁梫偑偁傞妏搙偼埲壓偺傛偆偵1.146搙偲偄偆
傕偼傗妏搙偲偟偰擣幆偱偵偒側偄丄偨偩偺揰偠傖側偄偺丄偲偄偆悽奅偵側傝傑偡丅
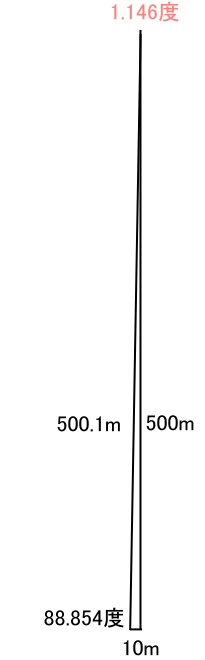
偪側傒偵悢帤偑傢偢偐0.2搙偢傟偰1.126搙偲撉傒庢偭偰偟傑偆偩偗偱丄
嫍棧偼510m偲10m傕偺岆嵎偑惗偠偰偟傑偄傑偡丅
偙傟偱偼20噏丄30噏偺嫍棧偺應掕偵偼巊偄暔偵側傝傑偣傫丅
偨偩偟丄偁傞掱搙傑偱偼偙偺揰傪曗姰偡傞曽朄偑偁傝傑偡丅
偦傟偑朷墦婡擻偱偡丅
偙傟傑偱偺婰帠偵偝傝偘側偔乮丠乯彂偐傟偰偄偨
懳暔儗儞僘仌愙娽儗儞僘偺搵嵹丄偙傟偑應嫍媀偵朷墦婡擻傪梌偊傑偡丅
3攞丄4攞偲偄偭偨朷墦儗儞僘偱偡偹丅
偡傞偲偳偆側傞偐丅
幚偼婎慄挿偝偲偄偆偺偼丄儗儞僘偺攞棪偵斾椺偡傞丄偲偄偆摿挜偑偁傝傑偡丅
側偺偱10m挿偺婎慄挿偺應嫍媀偱傕丄2攞朷墦偺儗儞僘傪愊傫偱傞応崌丄
10亊2亖20偱丄偦偺婎慄挿偼20m偲摨偠偲傒側偝傟傑偡丅
朷墦側偟偺20m應嫍媀偲摨偠惛搙丄偡側傢偪惈擻偑攞丄偲偄偆帠偵側傞偺偱偡丅
乮尩枾偵偼儗儞僘偺岆嵎偑弌傞偺偱丄幚嵺偵挿偄曽偑惓妋偱偼偁傞乯
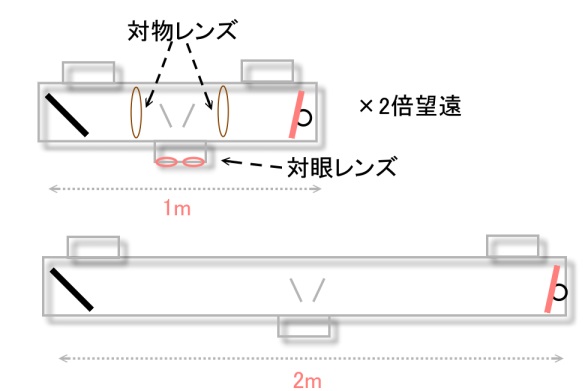
摏暆偵攞偺嵎偑偁偭偰傕丄抁偄曽偵2攞偺朷墦儗儞僘偑擖偭偰偄傟偽丄
婎慄挿偼摨偠偲偄偆埖偄偵側傞偺偱丄偦偺應検惛搙偼屳妏偲偄偆帠偵側偭偰偟傑偆丅
乮偨偩偟儗儞僘偺岆嵎偑偁傞偺偱姰慡偵懳摍偱偼側偄乯
偙偺攞棪偵傛偭偰堷偒墑偽偝傟偨婎慄挿偺偙偲傪乽桳岠婎慄挿乿偲屇傃傑偡丅
偱丄偙偺庤傪巊傢側偗傟偽懝偱偡偐傜丄
捠忢偺應嫍媀偵偼傎傏昁偢朷墦儗儞僘偑擖偭偰傑偡丅
側偺偱丄應嫍媀偺嫍棧應掕傪媮傔傞悢幃偼埲壓偑堦斒揑丄偲側傝傑偡丅

偲傝偊偢朷墦攞棪偑壛傢偭偨偩偗偱偡偑丄偙傟偱應嫍媀偼悘暘偲
幚梡揑偵偼側傝傑偟偨丅
偑丄偦傟偱傕傗偼傝20噏埲忋愭偼僉僣僀偩傠偆丄偲偄偆榖傪
師偺儁乕僕偐傜偄偨偟傑偟傚偆丅
NEXT