では、測距儀の基本的な原理について見ておきます。
ちなみに、今回説明するのは極めて原始的な測距儀の仕組みで、
実際のものはもう少し複雑。
が、やってることは同じなので、今回の話ではこれで十分と思ってください。
解説図の下の方にある横長の箱が測距儀です。
その左右にある出っ張りが目標を観察する窓だと作者は主張してます。
で、今回の目標である世紀末サンマドウロボウ ニャレンコフの位置を、
インターポールのカツノガスキーが測距儀で測量しているところです。
描いた本人がそう言ってるんだから、そうなんです。
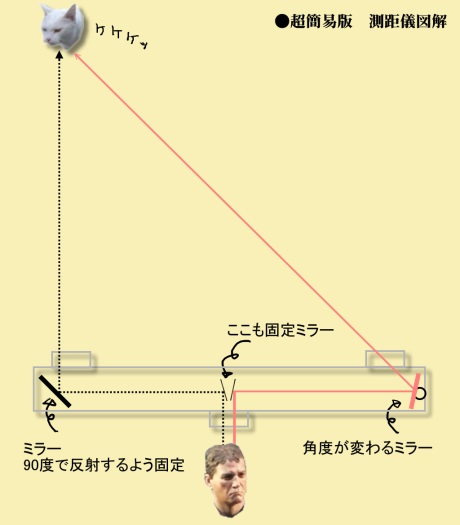
左右の窓から入ってくる光をミラーで反射して中央のファインダーに送り、
対物レンズ、接眼レンズ(図では省略)を通して目標を見る構造です。
この左右のミラーは、片方を固定し(図では左側)光を90度の角度で
中央ファインダー方向に送るようにします。
で、その反対側(図では右側)のミラーは角度が変えられるようにしておきます。
(実際の測距儀では左右のミラーが動くタイプもある。
これはあくまで原理の説明と思ってください)
で、左の採光窓を通してニャレンコフをファインダーに見ることが出来たら、
それはヤツが左の覗き窓の真正面に居ることを意味します。
この状態で測距儀を固定して、右のミラーでも
ニャレンコフが見えるように角度を調整しましょう。
で、右側でもヤツの姿を捉えることが出来たら、
これはニャレンコフを頂点に直角三角形が完成した、という事ですから、
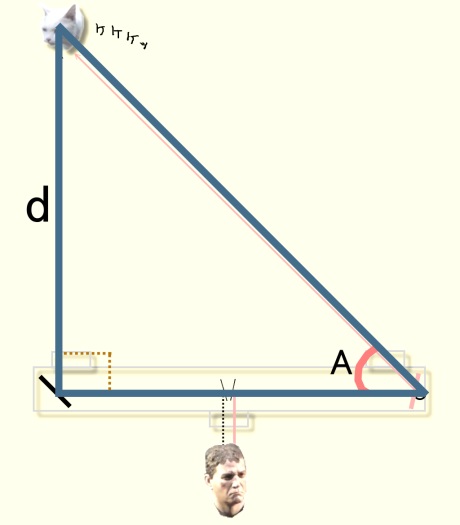
可動ミラーの角度(∠Aとします)が判れば、三角関数によって
相手までの距離がわかる、という事をになります。
これが測距儀の原理です。
∠A、その数字は目盛りによれば45度だったとしましょう。
やけにキリがいい数字ですが、話を単純にするため、目をつぶるのが大人です(笑)。
そして測距儀の長さは1mとします。
ええ、これも計算が楽だからですよ、もちろん。
今回の記事では、とりあえず三角関数(&逆三角関数)までは使わせてくださいませ。
直角三角形の3辺のそれぞれの比(互いに割り算した答え)は
辺の長さが変わっても常に一定である、というアレです。
このため、角度と1辺の長ささえわかれば、他の辺の長さが計算で求められます。
ここで、ニャレンコフまでの距離をdとしましょう。その方がカッコイイし。
で、三角形の底辺の長さは測距儀の長さだというのに注意してください。
となると目標までの距離dと、測距儀の長さの間には、三角関数タンジェント(tan)の
関係が成立するので、
tanA=距離(d)÷測距儀の長さ
であり、となると距離(d)は
距離( d)=tanA×測距儀の長さ
ですね。
つまり∠Aの角度さえわかれば、目標までの距離は
簡単に計算できてしまうのです。
測距儀の長さは1m。
そしてtan(タンジェント)Aの値ですが、
特定の角度に対応するtanの値は常に一つしかありません。
なので三角関数表でtanの欄を見るか、表計算ソフトや関数電卓で計算してしまえば、
難しい理屈は考えなくても計算はできます(笑)。
ちなみにtan45度は1です。つまり
d=1×1m =1m
目の前やんけ(笑)。
測ってないで捕まえたほうが早かった。
ここで、計測の基準となる距離、
今回なら測距儀の長さである1mを「基線長」と呼びます。
同じ測距儀を使ってる限り基線長は常に同数字になり、
tanAの数字も、特定の角度には常に同じ数字が対応しますから、
毎回、変化するのは∠Aの角度だけです。
つまり、同じ測距儀で計測する限り、∠Aの特定の角度は
常に同じ距離を意味する事になります。
なので測距儀の中にはあらかじめ計算して作っておいた
∠Aの角度ごとの距離表が入ってるのでした。
そして∠Aの角度が決まると、その表を使って
対応する距離が自動的に表示されるようになってるわけです。
が、これは近距離ならともかく、
基線長の数十倍を超える距離を測定するとなると、
かなり問題が出てくる話だったりもします。
NEXT