さて、連載第一回の最後に、自分の立ってる位置(高度)から
どれだけ先の地平線、水平線まで見えるのか、というのを解説しておきます。
別に知らなくてもいいや、という場合、読まなくても
今後の記事は理解できると思うので、とりあえず読み飛ばしてください。
ただ、理解しておけば、より面白くなるはずです。
さらに突然タイムスリップして戦国時代に漂流した場合なども、、
最低限の仕事をこなせる、というメリットもあります。
役に立たない未来からのタイムスリッパーほどカッコ悪いものはないですからね。
とりあえず大気の影響を考えない、理論値だけを出すなら、
その計算は意外に簡単で、中学レベルの算数、
ピタゴラスの定理さえ知っていれば答えは出ます。

これですね。
ピタゴラスの定理のいい所は、直角三角形で、2辺の長さがわかれば、
残り1辺の長さを計算で求めることができる、という点です。
では計算に使う「2辺の長さがわかっている直角三角形」をどうやって設定するんでヤンス?
というと、これは地球中心点と地表面を結ぶ線、すなわち地球の半径を使って
直角三角形を造ってしまいます。
下の図のように、水平線が地球上の一点に重なる以上、
水平線までの地球中心点からの距離は常に地球の半径と一致します。
さらに視点、つまり自分の居る場所までの長さは
「地球の半径+視点の高さ」で簡単に求められます。

視点から水平線を結ぶ線は地球の断面形、
つまり円への接線ですから、両者は直角に交わるので、
地球中心点、視点、そこから見える水平線の上の一点、
この3点を結ぶと、2辺の長さがわかっている直角三角形となるわけです。
長さのわからない残りの1辺、視点から水平線までの距離を知りたいなら、
もう計算で出せますね。
とりあえず見やすくするのと、こうしたほうが頭が良さそうに見えるので、
それぞれの長さをアルファベットの文字に置き換えます。
地球半径は「R」、地表から視点までの高さを「H」、
そして求めたい水平線までの距離をXとします。
これをピタゴラスの定理にあてはめ、Xを求めるには、
以下のような計算式に変形してやればOK。
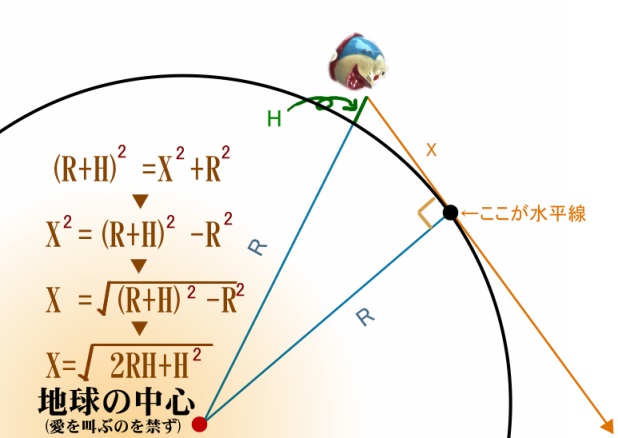
暗算は無理でも、計算機や表計算ソフトがあれば誰でも簡単に
計算できる数式となります。
早速、式に具体的な数字を当てはめて見ましょう。
まずはR、地球半径から。
ご存知の方も多いと思いますが、地球はうっかり自転なんかしてるもんだから、
その遠心力によって、わずかながら横方向にふくらんでいます。
よって、地球の半径と言っても、極点方向(南北)と赤道方向(東西)ではちょっと違います。
まあ0.34%前後の差で、誤差と言ってもいいのですが、
これから扱うのは海面上10~3000mくらいなので、無視するには微妙に大きな数字。
そこで両者の平均値、6367.5kmを今回の計算では使用することにし、
その誤差を最小限に抑えるようにしましょう。
次にH、視点の高さ。
この式では単位はkmなので、1mは0.001となるのに注意しましょう。
で、この数字は自分が知りたい高度の数字を入れればいいだけです。
海岸から見える水平線の距離が知りたいなら2mくらいの数字を入れればOK。
すると5.046kmといった答えになりますから、これが人間が海岸に立って見える
水平線までのおおよその距離です。
「ボクたちの未来は、あの水平線の向こうだよ!」
とか言うと意外にスケールの小さな話になるので、注意が必要です(笑)。
(ただし後で説明するように実際は光の屈折によりもう少し遠くまで見える)
ただし相手にもある程度の高さがある場合、話が異なります。
上で見た戦艦どうしが、相手の艦橋を見る場合などですね。
とはいっても考え方は単純で、
向こうから水平線までの距離を同じように計算し、
両者を合計してやればいいだけです。

水平線の向こうにある高度hの目標物までの距離をYとすれば、
上と同じやり方で簡単に地球半径を使った直角三角形ができます。
あとは同じ計算をやって出てきたYの数字と
自分から水平線までの距離Xを足してやるだけで答えは出ます。
ただし、鋭い読者の皆さんはすでにお気づきでしょうが、
「視点から水平線(目標物)までの距離」を正確に測るなら、
厳密には直線ではなく、地球円周上の長さ、
つまり弧の長さを求める事になります。
これを求めるには例の直角三角形における
地球中心点の角度がわかれば、
地球の全周は、半径(R)×(R)×3.14で出ますから、計算できます。
が、これをやるには三角関数の逆関数、
アークコサインの計算が必要で、正直面倒です(笑)。
しかも高度3000mレベルから視認距離を計算した場合でも、
ここで紹介した計算法と比べて60m前後の差しかでません。
(195.43kmと195.36m)
よって、上記の計算で十分と判断していいと思います。
ただし、高度数万メートル、とかになった場合は、
キチンと計算した方がいいでしょう。
もう一つ。
最後に出てきたX+Yの合計を求める数式で、Hとhを2乗して足しますが、
これはその答えを足す相手、2RHに比べると、
高度100m(0.1km)くらいまでなら非常に小さな数字で、あまり意味がありません。
なので、この数字を無視して、

として、視認距離(キリのいい113を係数にすることが多い)を求める数式もあります。
専門書籍などでは、説明なしにいきなりこの式が出てる場合が多いですし、
実用上、ほとんど問題ないので、こっちで済ましてしまうのもありでしょう。
ただし、両者が高度1万メートル、とかいう大きな数字になると話は別で、
この場合は図の中の式を使わないと、数㎞の誤差がでます。
と、ここまで書いておいてなんですが(笑)、
これはあくまで理論値、大気が無い場合、の計算となります。
さらに地球の半径をどう計算するか、によって結構誤差が出ます。
なので、実際の計算では次のページで見る式が多くなるようです。
NEXT