さて、なんでボイドがそこまで機体の重量増加を嫌ったのか、を少し詳しく考えて行きましょう。 結論から言ってしまうと、戦闘機では旋回中の加速度、Ｇが極めてデカくなるからです。 死ぬか生きるかの空中戦、あるいは無数のミサイルを回避する旋回では9G程度まで負荷が掛かるのですが、これは機体の「重量＝機体に掛る力の大きさ」が9倍にまで跳ね上がる事を意味します。すなわち19トン(tf )の離陸「重量」で飛んでるF-15が9Gの旋回を掛ければ、地上の9倍、171トン(tf )の力を受けます。 ちなみに先に見たボイドがF-15から外したかった足掛けの総重量、200�sfでも9Ｇ掛けた場合は1.8トン(tf)の「重量＝機体に掛る力の大きさ」になってしまうのです。 馬鹿みたいにデカくて重い印象がある日産のGTRでもその重量は約1.7トン(tf )前後となっています。 よって9Gで1.8トン(tf )の負荷が増えると言うのは、デブが乗ったGTRを抱えながら限界性能の旋回に挑むようなものなのです。 ところが機体の運動を支えるエンジン出力はどれだけ高いGが機体に掛かろうが全く変わりません。 現在最強クラスの出力を持つF-135エンジンでもアフターバーナー点火の最大出力で約19.5トン（tf =191kN）しか無いことを考えると、「重量＝機体に掛る力の大きさ」がトン単位で上昇した場合の負担増加がどうなるか、想像がつくでしょう。 エンジンに掛かる負担を考えると厳しい、運動性も落ちる事になる、というのは理解していただけるかと。ゆえにボイドは少しでも軽くしたかったのでした。 もっとも、機体を直接エンジン推力で持ち上げているワケでは無く、推力で機体を加速、生じた速度を運動エネルギーとして蓄積、それを主翼で揚力に変換して飛んでるわけですが（F→F*l= E→F）、それでも影響は小さくありませぬ。 ■質量と重量の違い この辺りの話を理解するには、どうしても「質量」と「重量」の違いを理解する必要があるので、これも見て置きます。 「質量」と「重量」は、どちらも長年に渡り慣例的に同じ単位、「kg」を使って来たため混乱しやすくなっていますが、本来は完全に別次元の量なのに注意が要ります。つまり「時間」と「長さ」のように完全に別の量であり、両者を同じ単位で表記するのは本当なら狂気の沙汰なのです。これは3時間＝3メートルみたいな話であり、力学的に言えば完全に狂ってます。「質量」と「重量」は三毛猫とハレー彗星くらい違うんですよ。 kgは本来、「質量」の単位なので、こちらに使う場合は何の問題もありません。 対して「重量」の単位は本来なら、kgw か kgf を使う必要があります。そもそも重量＝力の大きさなので、そのままkg m/ss 、あるいはＮ（ニュートン）単位の表記でも問題ありません（ただしこの場合は後で見る理由により数字は9.8倍になる）。すなわち重量は本来、「力」の大きさなのです。ところが長年にわたり、慣例的に「重量」も単にkgあるいはｔ（トン）と表記されて来たため、話をややこしくしてしいます。その違いをキチンと理解しないと今回のお話は理解できないので、少し詳しく見て置きましょう。 まず基本となる「質量」は大宇宙の隅々に至るまで不変な「動かしにくさ」を示す単純な量です（スカラー）。 対して「重量」は重力加速度が「質量」に掛かって生じさせる「力」であり、下向きの方向を持ちます（ベクトル）。地球上では垂直下向きの力であり、その力の大きさ＝重量となります。当然、力である以上、可変であり、重力加速度の大きさにより変化します。すなわち100kgの「質量」は地球でも月でも同じ量ですが、「重量」は異なり、重力加速度が小さい月の上の方が軽く、簡単に持ち上げられるのです。 この辺りをもう少し具体的に説明しましょう。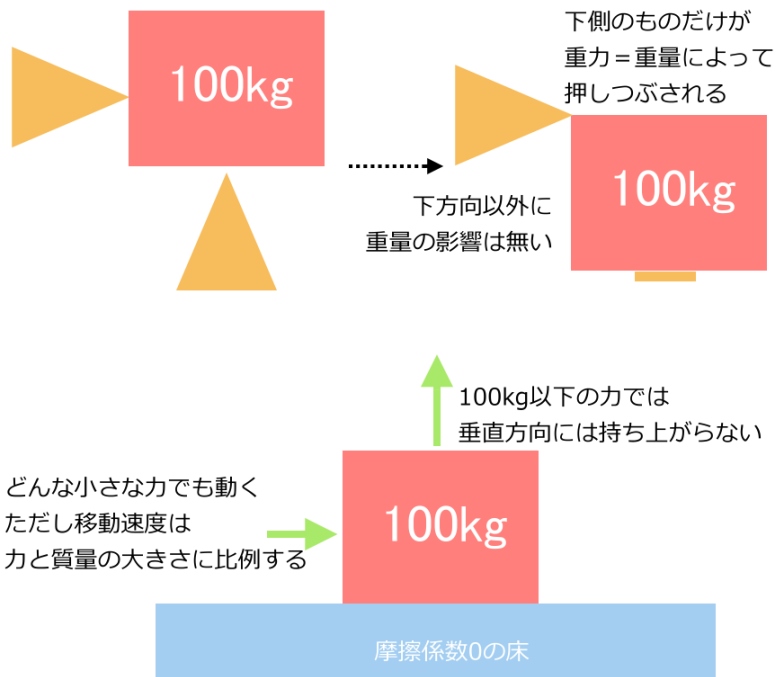 100kgの「質量」が無重力の宇宙空間に浮いてる場合、一切力は生じないので上下左右どの方向からそっと触れても何も起きません。ところがこれを地球上に持って来ると、垂直方向に重力加速度が掛かり「重量」 が生じます。よって下側に回ると、その力で押しつぶされてしまう事になるので要注意です。ただし力は下方向のみに働くため、それ以外の方向なら宇宙空間と同じく何の力も受けません。 同じように地球上で奇跡的に摩擦係数が0の床があり、そこに100kgの質量の物体を置くことを考えます。 この時、重量＝力と正反対の垂直方向に持ち上げるには100kgwを超える力が必要で、それ以下の力では動きません。対して力＝重量が生じない横方向にならどれほど小さな力で押しても、例え1/100でしかない1�sの力で押しても、スッと動くのです。ちなみに無重力状態なら、全方位に対してこの条件が成立します。 この時、どこまで加速できるかは押した力の大きさと質量の大きさに比例するため、質量は「動かしにくさ」を見る量なのです。対して重量はすでに見たように下方向に掛かる「力の大きさ」を意味します。すなわち「動かしにくさの量」では無く、「下向きの力の大きさの量」です。全く別物ですね。 とりあえずこの辺りの質量と重量の特徴について簡単な図にすると、以下の通りです。   さて、重量＝力ですから、これを求める式は、ニュートン力学の基本中の基本、 質量（m）×加速度(a)＝力（F） に重力加速度9.8m/ssの係数9.8を掛けてやればよく、 質量（m）×加速度(g)×9.8＝重量(Wg) ですね。 この地表付近の重力加速度9.8m/ss、あらゆる物体を1秒間に9.8m/sまで加速させる加速度をを1単位とするのが皆さんおなじみ「G」であり、すなわち1G=9.8m/ssです。 とりあえず上記の式から1kgの質量は地上付近では重力加速度（1G）により 9.8kg m/ss＝9.8N（ニュートン）の力を受けている事が判ります。この「重量＝力の大きさ」を示すのに長年の慣例で「質量」と同じ「kg」を使っているのが問題なのです。それだと「質量1kg＝力の大きさ9.8N」であり、繰り返しますが30年＝120kmみたいな無茶苦茶な話になります。 厳密には重量は1kgf、または1kgwと表記するのが正しく、この1kgfは、1kgの質量に9.8m/ssの重力加速度（1G）が掛かった力の量（＝9.8N）に等しくなります。すなわち「重量」1kgとは、本来は9.8Nの「力の量」であり、繰り返しますが「質量」1kgとは完全に別物です。長年の慣例なので、今更どうしようも無いのですが、とりあえずこの記事では両者を厳密に区別しますから、以後もご注意願います。 ちなみに重量＝力なら、民間宇宙旅行には行けない一般庶民である我々は（私は違う、という人は是非当サイトの増刊号のお買い上げをお願います）、一年365日（うるう年を除く）、その力を全身で受け止めているわけです（ただし厳密言うと地球引力圏を脱出しない現在の宇宙飛行は床と一緒に自由落下してるに過ぎず、その力を受け続けているが）。 ところが日常生活では誰もが地面や床や筋斗雲の上に乗っているため、重力加速度から生じる重量を力として実感しにくくなってます。この点は下に支えが無い状態、すなわち深い落とし穴などを利用すると判りやすいでしょう。その場合、重力に盛大に引っ張られて地球の中心点に向けて落下して行くことになり、なるほど重力加速度の力で引っ張られて加速し続けておるわいホッホッホ、と体感できる事になります。ただし下手すると死ぬので、この点の確認は自己責任でお願いします。 せっかくなので少し触れて置くと「質量」が完全不変なのはニュートン力学の範囲内までで、厳密には慣性系の重力（一般相対性理論）と速度（特殊相対性理論）の影響を受けます。それでも地球に居る状態で、人類が到達可能な光速の1/10,000前後、秒速30km＝時速10万800キロメートル程度の観測までなら影響を無視できますから、今回のお話では考えなくて大丈夫。 ただし例外的に原子時計級の正確な時間調整が必要な、地上の物体をメートル単位で捕らえるGPS衛星は重力（一般相対性理論）、速度（特殊相対性理論）の両者の影響を避けられず、その補正を行っています。これは身近な相対性理論の活用の一つで、未だに定期的に出て来るアインシュタインの相対性理論は間違いだよ説を一蹴する根拠の一つとなっています。 よって21世紀の社会生活だと相対性理論、しかも「一般」の方まで必須なのでした。学校で習った事は社会生活で不要なんてことは無いのよ。ちなみに一般的なGPS衛星の速度は秒速4km以下であり、どれほど精密な計測をやっているかが判るかと。 以上、脱線終了。 ■重力加速度と加速度 さて、ここからは戦闘機の運動中に掛かる加速度、旋回中のGに関して考えてゆきましょう。 とりあえず「重量」と「力」の大きさを求める式はどちらも、質量（m）×加速度（a）なのですが「加速度」には二種類あるのに注意が要ります。 まずは地球などの重力が物体を引き寄せ加速させる重力加速度（Gravitational acceleration）、そして人間の筋力や各種エンジンが物体に加える力で加速する単純な加速度 （Acceleration）です。重力加速度は地球上では9.8m/ssでほぼ不変ですが、単純な加速度は運動によっていくらでも変化します。そして前者は位置エネルギーを、後者は運動エネルギーを発生させます。 ちなみに片や万有引力によるもの、片や熱エネルギーによる運動によるもので、冷静に考えた場合、とても同じものとは思えないのですが、両者が等価である、すなわち本質的に同じものだ、というのは厳密に証明されています。ただしその証明は私には説明できるようなモノで無いのでここでは省きます（手抜き）。 さて、その「加速度」の種類によって生じる力が「重量（重力加速度）」と単純な「力（加速度）」 に分類されるわけですが、既に見て来たように両者は全く同じ次元の量です。このため重力加速度を基準とする数字、すなわち9.8m/ss＝1G という単位を利用して話を進める場合、この二つは完全に同じものとして扱えて便利です。よって以後、記事中のあらゆる加速度の単位は ■9.8m/ss＝1G として進めてゆきます。 ただしGは加速度、運動変化の量の大きさであり、力の大きさでは無いのに注意してください。 すなわち4Gで生じる力、という記述は正しいですが、4Gの力というのは間違いです。例えば100kgの質量と200kgの質量の物体に同じ4Gを掛けた場合、400kgf（＝100kg×4N）と800kgf（＝200kg×4N）の力がそれぞれ生じており、同じ4Gの加速度運動でも力の大きさは全く違いますから要注意。 さらに常に下向きの重力加速度とは異なり、運動によって生じる「加速度」は機体の姿勢により、あらゆる方向に発生します（厳密には機体が生じさせる揚力の方向による）。さらに重力加速度のように常に1Gで固定では無く、消費できるエネルギーがある限り上昇する、という特徴があります。 ちなみに「加速度」と言う日本語から誤解を受けやすいのですが、この量は速度の増減だけを示すものではありません。 ニュートン力学においては慣性状態を破る力が加わって生じるのが加速度でした。 慣性状態には「完全に静止」と「等速運動」つまり同じ速度でずっと動いてる状態の二種類があり、どちらも加速度はゼロで力を生じたないため、外が見えない箱の中等では自分が静止中なのか等速運動中なのか判断する事はできません。 ここに力を加えた結果、生じるのが加速度です。 普通に速度が増減する場合、前後にグッと力が加わるため、これによって加速、または減速（マイナス方向の加速）をしたと中の人間は気が付きます。そして等速運動の物体が曲がった場合も力が生じるため、中の人間は曲がったな、と気が付きます。つまり、「曲がる」のもまた力が生じる加速度運動なのです。 ■U.S. Air Force photo by Staff Sgt. Trevor T. McBride このため戦闘機などが旋回に入る時、すなわち曲がる時には必ず機体に加速度が生じます。既に見たように、これを重力加速度を基準とした倍数で示すのが「G」となります。機内に潜むゴキ●リの数では無いのに注意してください。 これを「機体に掛る力の大きさ」に換算するには、機体重量×G×9.8　という計算が必要なのですが、同じ機体ならG以外の数字は一定であり、だったら単純な整数「G」で示す、加速度表記で統一する方が便利、という事になります。 何度か指摘してるように空中戦、あるいは誘導ミサイルを回避するための急旋回では軽く6Gを越え、最大だと9G、世界記録レベルだと12Gまで掛かる事があるわけです。当然、その数字の倍数だけ機体に掛る力が増えます。よって9G旋回では地上駐機状態の9倍の「重量」になっていると考えてよく、地上で200kgfの重量でも、生きるか死ぬかの9G旋回中には1.8tf もの負担になる、というのはこれが理由です。よってそりゃ死活問題になるよね、という話なのです。 この増加分をエンジン出力だけで支え続けるワケですから、いろいろ大変であり、よって機体重量を少しでも減らしたい、すなわち機体を少しでも軽くしたい、となります。この点こそがボイドの狙いだったのでした。