
■原点回帰2025-2
さて、今回は「絵の描き方」を論理的に解析して行きます。
このため全人類の128%が興味ないと思われる話、筆者がどうやって絵を描き始め、そして今どうやって描いているのかを説明して行くことになります。この点はご容赦くださいませ。自分でもどうかと思うんですが、何度考えてもそれが最も効率がいいのです。では、さっそく行って見ましょうか
筆者がまだ花も恥じらう美少年(美の少ない年頃)の小学生だった当時、子供向けの漫画雑誌には大抵、漫画の描き方講座が年に一度は掲載されていました。でもって当時、穢れを知らぬ田舎の子供だった筆者は言われた通りにやってみたのです。その手の記事においては平面図形で漫画のキャラクターは出来ているとされ、丸と四角とあとは三角くらいで人間の絵は描けると述べられておりました。マジかよ、それなら俺にもできそうじゃん。でもね、その完成図を見てみると、だいたいこんな感じの絵が掲載されていたのです。
ちなみに筆者は絵を描く才能があるのではなく、正確には立体を平面に写す「感覚」が人より優れているだけです。よって前回見たように転写の能力は全く無いのですが、立体を平面に再現する点では幼少の頃からウットウしいまでの嗅覚がありました。このため見た瞬間に、こんな人体が存在してたまるか、馬鹿にしてんのかとしか思えず、以後、絵を描く事には興味を無くします。
まあこの辺りは前回も書きましたが、漫画なら最悪、絵が上手い下手どころか、キャラの顔がアルファベット文字でも成立するのでこれで問題ないし、図形と記号の塊、すなわち作図であって作画ではない「絵」は今でも世の中に溢れてます。よって正しい、間違っているの問題ではなく、ただ個人的に好きではなく、興味も無かったのです。
そんな筆者が絵を描くようになったのは、やがて出会う恩師の美術教師の熱心な指導があったから…といった感動秘話は一切なく、それをでっち上げる情熱もないので、さっさと結論から述べてしまいます。本来、絵を描くことに全く興味が無かった筆者が、これは挑戦してみる価値があるかもしれん、と思ったのは、小学校4年時あたりの算数の授業中の事でした。その時、先生がこの地球上には長方体という物がある、それは四角い箱の事である、として以下のような図を黒板に描いたのです。
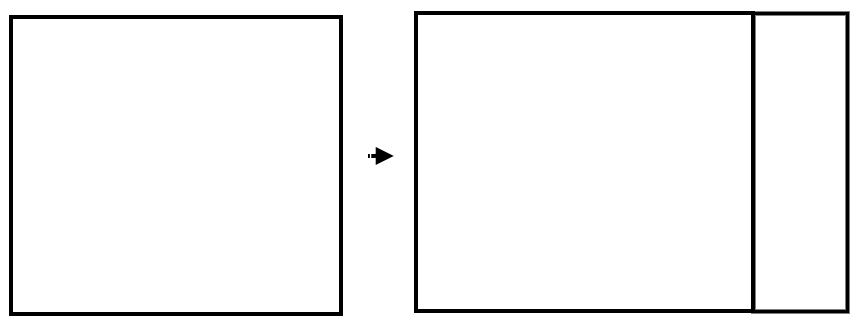
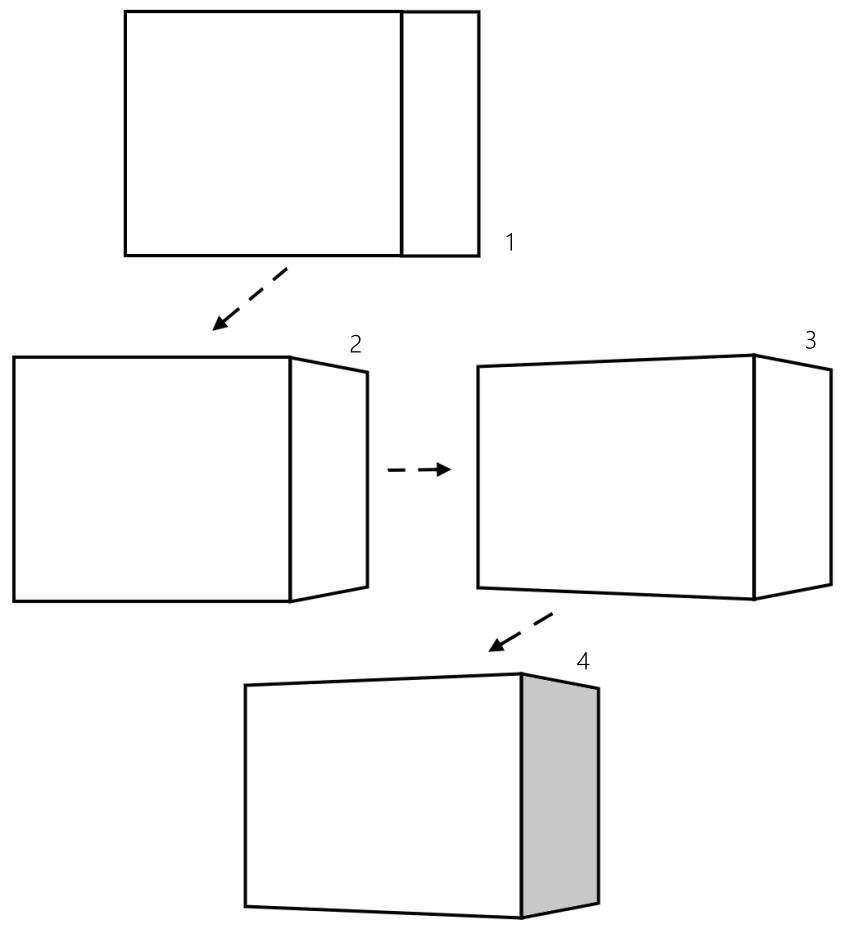
生きる事を含めあらゆる点で不器用な筆者は、この図を写しとる取るにあたり、片側が台形のような歪んだ形状になってしまいました(図中2)。まあモノグサなので定規なんて全く使いませんでしたし。ところが、歪んでいるはずのこちらの方が黒板の絵よりずっと箱に見えるじゃん、と気が付いたのです。それはナゼか。どうも横線を平行線ではなく斜めに傾けたからではないか、と恐るべき推理力で見抜いた筆者は、残る左側の長方形の横線も少し傾けて見たのです(図中3)。すると!これは!箱!誰が見ても圧倒的に箱!!すなわち平面の中に立体が完全に再現されている!感動のあまり隣の席の中村に見せてやったのですが中村は不幸にして馬鹿だったので、その凄さが判らず、何も言わずに無視しました。許そう、だが忘れぬ。
このため、しばらく授業そっちのけで立体の再現に夢中になるのですが、何気なく横面を鉛筆で塗りつぶしたら(図中4)、さらに立体的に見える事に気が付いたのです。こうして小学校の算数、立方体の授業の中で筆者は立体が平面に再現できること、しかもそれが思った以上に簡単な事に気が付き、以後、この作業に熱中する事になります。
「線を傾ける事による奥行きの再現」「陰影による面の再現」を「発見」した筆者は四角でこれだけの事ができるなら円でも行けるんじゃない、と思いつきます。幸い、コンパスを使えば好きなだけ円は描ける。ですが円には側面が無いため、上記の大発見は使えない事にすぐ気が付くはめに。では、どうするか。
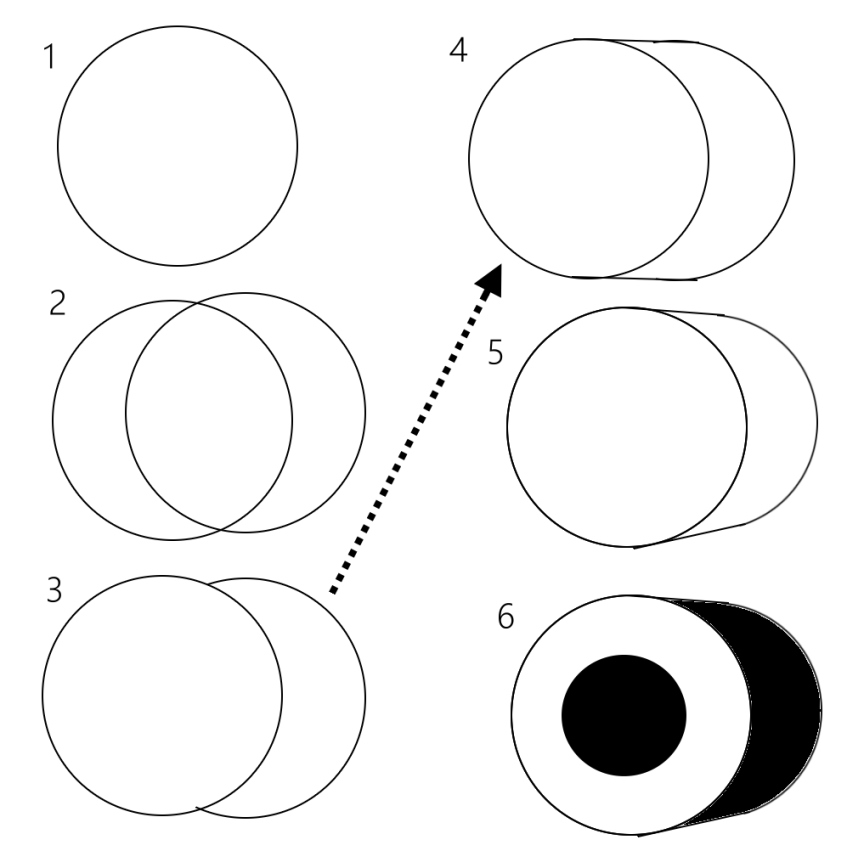
間もなく円を二つ重ね(上図2)、重なっている部分を消せば(上図3)立体に見えない?と思いついたのですが、実際にやって見たらそうでも無かったのでした。ただ左右の円を直線で繋げば何かの立体にはなりそうだと思いついたのでやってみる(上図4)。ところが円は同じ大きさなんですが、目の錯覚で後ろが大きく見えてしまい、どうも立体感が出ない。そしてここでヒラメくのです。だったら後ろの円を小さくしてみればどうか、と。でやってみたところ(上図5)、おお、立体的な円柱が爆誕したではありませぬか。これで面が出来た以上、そこを影にして見たのですが、その上で真ん中に小さい円を追加すると(上図6)、なんと海苔巻き寿司が平面の上に完全再現されてしまったのです(完全再現の定義には個人差があります)。
マジか!箱に加えて海苔巻き寿司まで紙の上に完全再現できるなど、神にも匹敵する奇跡ではないかと筆者大興奮となりました。もはや負ける気がしない。
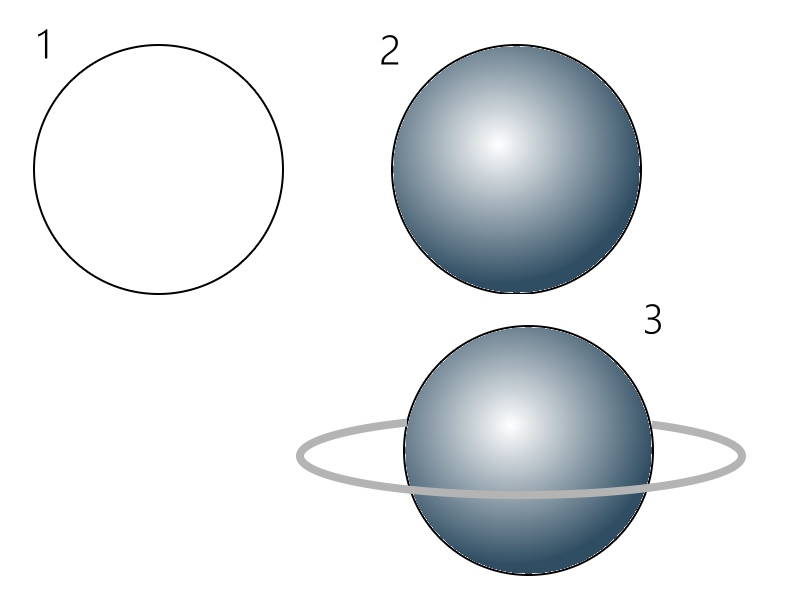
その数日後のアンニュイな午後、さらなる奇跡が筆者を襲います。それはなんとなく鉛筆で円を塗りつぶした後に起こりました(奇跡の感じ方には個人差があります)。特に何も考えずに消しゴムをかけたのですが、その時、最初に一部だけ消した状態を見て、あ、これは球だと気が付いたのです(図中2)。円には側面がないので奥行きも陰影も表現できないと思っていたんですが、明暗のグラデーションで立体感が生まれ、ただの円が球体に早変わりすることを発見したのでした。なんか輪っか付けたら、どこからの謎の惑星っぽいし(上図中3)、これはもう大宇宙を手に入れたと言っても過言ではあるまい、と確信します。我は神の視点を手にしたと思いましたね、ええ。
こうして小学算数の授業を通し「線を傾ける事で奥行きを」「面の陰影でさらに立体感を」「奥にある面を小さくすることでより自然な奥行きを」「陰影で曲面を」それぞれ表現できることを一気に発見したのでした。圧勝と言うほかない怒涛の展開だったと言っていいでしょう。まあ先生はそんな事を教えたつもりは微塵もないでしょうし、文部省(当時)としてもそんな気づきは期待もしてなかったでしょうが、事実は事実。よってありがとう小学算数、とこの場を借りてお礼を申し上げます。
そして冗談でもなんでも無く、基本的にはこの四点を利用して今でも絵を描いています。私の絵のすべては小学算数に由来すると言って過言では無いのです。すなわちあれから40年以上が経過した今も小学生レベル。次はその辺りの手法を具体的に見てゆきましょう。