さて、エネルギーの話の最後に仕事率(P)という
エネルギーに関する、最後の「量」を見ておきましょう。
馬力だ、ワット(W)だという、なじみ深い単位で示されながら、
実はあまりよく理解されて無い「量」がこの「仕事率(P)」で、
その略号はPです。
これは英語のPowerの頭文字なんですが、
Powerには、能力、成し遂げる力、といったニュアンスがあるので、
そういった意味で使われるPowerで、力学的な力の意味ではありません。
力学的な力はForce となります。
余談ですが、英語のHigh power を日本語でハイパワーと書くと、
なんだかノーテンキな力持ち、という印象になりますが、
厳密には「何かをやり遂げる強い能力を持つ」といった意味で、
単なる筋肉バカではないニュアンスがあります。
さて、その仕事量(P)を理解するには、
ここまで見てきたエネルギー(E)と仕事(W)の量を求める
基本式を再度確認するところから始めましょう。
仕事=エネルギーを求める基本式は、
力(F)×距離(L)=エネルギー&仕事
でした。動かした距離が問題になるのでしたね。
これを速度から求める場合も、結局、
力による加速が終わった段階の速度ですから、
それはどれだけの距離を移動したか、を別の面から見てることになります。
さて、ここで2人の人間が1kgの物体に力を加えて10mの距離を動かす
仕事(W)をした、という話を考えてみます。
この時使えるエネルギーの総量は50J(ジュール)だとしましょう。
ただし、これは摩擦なし、重力なし、空気抵抗なしの空間で行なわれる
必要があるので、コイツらホントに人間か、
という疑問が出て来ますが、そこら辺りは目をつぶります…。
ざっと図にするとこんな感じですね。
Aさん、Bさん共に、50Jのエネルギーを使って、
1kgの物体を10m動かしたのですから、
その行なった仕事(W)の量は同じです。
が、それはあくまで距離しか見てない場合。
この場合、その時間はどうなるのか?

ここで、Aさんは最初の1秒間で全てのエネルギーをつぎ込んでしまい、
その後、物体は慣性で飛んでゆく、としましょう。
この時の、彼の作業時間を考えます。
使えるエネルギーが50Jの時、
1kgの質量の物体の最大速度を「n」とすると、
運動エネルギーの式から、
1/2×1kg×n m/s×n m/s=50J
nn=50×2÷1
n=√100=10m/s
が、全エネルギーをつぎ込んだ段階の最大速度ですね。
Aさんは最初の1秒間で、ここまで行ってしまう、という事ですから、
その加速度=10m/ssという事になります。
そして、その間の移動距離は、
1/2×速度(V)×時間(t)=移動距離(L)
でしたから、
1/2×10m/s×1 秒(s)=5m
つまり、1秒間に、5m進んだ段階で加速は終了し、
残り5mを10m/sの速度で慣性移動する、という事です。
5mを10m/sで移動するなら、0.5秒で移動が終わります。
となると10mの地点まで1kgの質量の物体を運ぶのに、
合計1.5秒かかった、という事になります。
■Aさんの作業時間 1.5秒

対してBさんは2秒かけてエネルギーを使いきったとします。
その段階の最大速度、10m/sは同じですが、
そこまでの移動距離「n」を考えると、
1/2×速度(V)×時間(t)=距離
なので、
1/2×10m/s×2秒(s)=n m
10m=n
つまり2秒かかって、全エネルギーを使い切った段階で、
Bさんは10mの距離に到達します。
よって、Bさんは1kgの質量の物体を10m運ぶのに、
2秒かかったという事になります。
■Bさんの作業時間 2秒
という事で、同じ50Jのエネルギーを使って、
同じ1kgの物体を10mずつ動かす仕事をしたのですが、
Aさんはこれを1.5秒で片付け、Bさんは2秒かかって片付けました。
仕事(W)量だけを見れば同じ量ですが、
両者を同じと見なすのは、やはり無理があるでしょう。
Aさんなら、作業後トリプルスピンからのジャーマンスープレックスも可能ですが、
Bさんにはそんな余裕は全くありません。
となると、同じエネルギーを使って同じ仕事をしても
どれだけ早く、つまりより効率よく作業できたか、
という点を考える必要がありそうだ、ということですね。
それを測る量が仕事量(P)なのです。
よって、それを求める式は、
仕事(W)÷時間(t)=仕事量(P)
という単純明快なものになります。
これは蒸気機関の効率化を図ったワットが、
自身の機械の性能を表すために考え出した
新たな次元の量だと言われています。
実際、彼の会社、ボールトン・ワット社は馬力(hp)という
仕事率の単位を世界で初めて使った会社でしょう。
ついでに、もう皆さん、慣れたと思うので(笑)、
さっそく式の変形をやってしまうと、
仕事(W)=力(F)×移動距離(L)
の式から右側の数式だけもらって来てしまいます。
となると、仕事率を求める式は次のように変形できます。
仕事(W)÷時間(t)=仕事量(P)
=力(F)×移動距離(L)÷時間(t)
=力(F)×速度(V)=仕事量(P)
となるわけです。
最後は移動距離÷時間が速度になってます。
つまり、仕事(W)の効率を見る仕事率の量ですが、
同時に力(F)を速度(v)で積分したものである、となるわけです。
これで力の積分は、時間(運動量)、距離(エネルギー&仕事)、
そしてこの仕事率の速度、と3種類が揃った事になります。
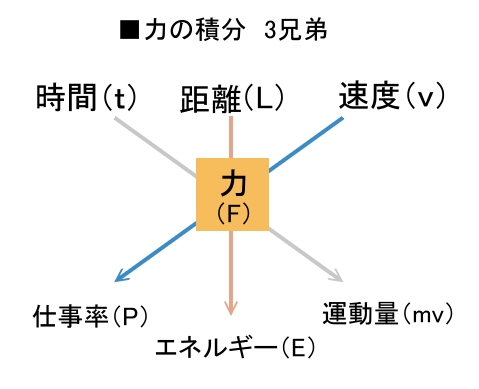
簡単な図にしておくと、こんな感じですね。
上のそれぞれの量を力で掛け算、積分すると、
下の各量になるわけです。
NEXT