さて、今までは慣性の運動、等速直線運動から始まり、
加速度を伴う(加速&減速)直線運動までを見てきました。
が、世の中には曲がる、という運動もあるわけです。
というか、たまには曲がらないと人生エライことになります。
でもって単に曲がる、というだけの話なんですが、
それだけで一気に話が難しくなる、
というのもニュートン力学の特徴なのです。
これを本格的にやると、またも終わらなくなるので(涙)、
そのほんのサワリ部分のみ、もっとも単純な
等速円運動を少しだけ見ておきましょう。

同じ速度で、中心点から一定の半径を保ち、
ぐるっと円を描く運動が等速円運動です。
現実世界でこんな運動はまず見かけませんが、
理屈を考えて行くには単純で、いろいろと都合がいいのです。
で、以前にも書いたように曲がる、
というのは等速で運動しても、加速度運動となります。
物体の質量に曲げる力がかかって加速度が生じるからで(力(F)=質量(m)×加速度(a))、
円運動の場合、円の中心点方向への力が常にかかった状態になります。
これを今回も空気なし、重力なし、根性なしの慣性空間において、
慣性飛行中の物体から考えて行きましょう。
その飛行中の物体に対し垂直方向に惑星の引力(重力)がかかって
円運動に入った、とします。
ここでは、垂直方向に力が加わわる、というのが重要です。
垂直方向の力は慣性運動の進行方向に対し、
重なる事も、対抗する事も無いため、
加速の力にもならず、逆に減速も起こさないのです。
慣性運動の速度はそのまま、円の中心方向に引きつける事になります。
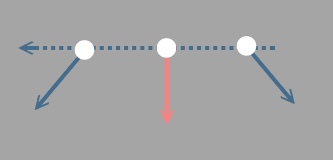
慣性により停止中、または等速直線運動中の物体に、
外部から力が加わった場合を考えます。
この時、重力が斜め方向を向いていると、
前進、または後退を補助する力として働いてしまうため、、
物体は斜めに進みながら、ひたすら加速、または減速に入ります。
が、垂直方向に力が加わった場合は、
進行方向に対して直接の影響がないため、
曲げようと引っ張る力、慣性の運動、
両者はそれぞれが独立して物体を動かして行く事になります。
この結果、加速も減速も無い等速運動のまま、
重力に引かれて内側に曲がり、後は引力の方向、中心点を回る円運動へと入ります。
ちなみにこの図は、慣性運動に対する力の流れを見てるだけであり、
力のベクトルの説明ではありません。
慣性の運動は力が0の運動ですから力のベクトルは存在しないのです。
よって両者の合成もできません。
合成が行われるベクトルは、速度なのです。
この引力によって円の中心方向に速度が生じた後で、
慣性運動の速度との合成が行われます。
この点は注意してください。
この結果、慣性と重力は独立して物体に働きかける形になります。
これが連続して続く結果、円運動へとなってゆくのです。
つまり、常に前進しようとする慣性の運動と、
それを円の中心方向へと引き付ける力が同時に働いて、
円運動は生じるわけです。
とりあえず、そこら辺りを図で見てみましょう。
でもってもう一度書きますが、これは力のベクトルの説明ではなく、
物体の動く方向とかかる力の方向を
図にしただけですから、注意してください。
慣性運動中である限り、そこに力は存在しないのです。
よって等速円運動は慣性運動が独立したまま力を受ける、
というやや特殊な運動となっています。

ここで内向きの重力と、物体を直進させる慣性は
常に物体にかかり続けるのだ、というのに注意してください。
途中でどちらかが欠けると円運動は崩壊します。
もし重力が消えたなら、物体は等速直進運動に戻って飛び去りますし、
慣性の運動が消えたら、重力に引かれて
ひたすら重力源に向けて落下する事になります。
ただし、円運動に入るには物体の質量と重力のバランスも問題になり、
一瞬、重力に掴まっても円運動にならず振り切ってしまう場合、
逆にあっという間に重力源に向けて落下して行く場合があります。
が、これも話を単純化するため、ちょうど円運動にはいる
バランスだった、と考えておいてください(手抜き)。
さて、物体の慣性運動を妨げて円運動に引きずり込む力、
これを円の中心方向に向う力、という意味で「向心力」と呼びます。
今回の話では重力がそれに当たりますね。
同時に、これが発生させる加速度を「向心加速度」と呼びます。
この向心加速度があるゆえ、円運動は加速度運動なわけです。
NEXT