ここで円運動で常に中心方向にかかり続ける力、
すなわち向心力の量を求めて見ましょう。
これを求めるのは速度もベクトルなのだ、というのと
そこから加速度を読み取れるのだ、という点の
とても分かりやすい例の上、向心加速度も重要な量ですからね。
今回も例によって計算を簡単にするため1kgの質量を持ってる物体が、
10m/sで等速直線運動中、星の重力に掴まる、と考えて行きますよ。
これは等速円運動となります。
(厳密には楕円運動に入る可能性も高いが、今回は考えない)
でもって、繰り返しますが慣性は「力」ではないので扱いがやや面倒です。
あくまで運動を維持しようとする不思議な原理なのだ、と考えてください。
速度の変化が生じるまで、運動中でもその力はゼロなのです。
実際、その正体が何かは誰にもわからないでしょう。
ついでに以前に触れた遠心「力」は、実は慣性運動を
回転運動中の非慣性系から見ただけなので「力」ですらありません。
ここら辺り、慣性の力という言葉、まぶしい暗闇みたいな意味不明の
言葉で説明されてたりしますが…。
まあ、ニュートンの理論体系というのは、どこか不完全な印象が残ります。
とりあえず、等速円運動の向心力を求めるには、力の基本となる加速度、
ここでは向心加速度を求める必要があります。
でもって、加速度は速度の単位時間あたりの変化率でしたね。
つまり、等速で円周を運動中の物体から、
速度の変化を読み取る必要があります。
…なんだか、出来の悪い一休さんのトンチのようですが、
速度をベクトルで表して考えると、答えが見えてきます。
ここで向心加速度を求めるのに、ベクトルの合成が登場します。
これは例の力のベクトルで既に見たものですが、
今回は力ではなく、速度のベクトルで考えます。
ベクトルは方向を持った量、でしたから、力だけでなく、
進行方向を持つ速度(V)、運動量(mv)もベクトル量なのです。
よって、矢印で向きを、線分の長さによってその大きさを表現できます。
今回の速度のベクトルの基本的な考え方としては、下の図のような感じになります。
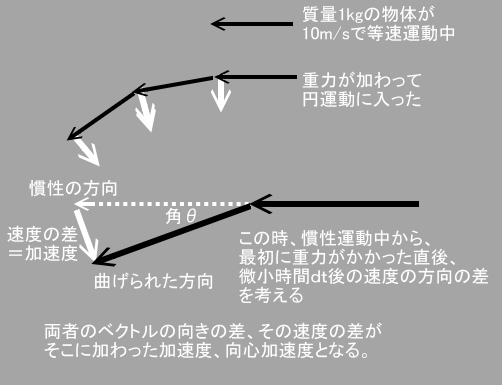
先に見たように、垂直方向の重力は慣性の運動速度に無関係であり、
よって物体の速度は常に一定のままですから、重力に捕らえられた後も、
1秒間における速度のベクトルの大きさは同じになります。
ここに速度の差はありません。
が、両者のベクトルの向きは異なるのです。
この向きの差の量が速度差であり、すなわち加速度となります。
速度が同じでも、ベクトルの向きが異なると、速度差は生じるのです。
さて、一番下の図の左側、この角θは
微小時間dt の間に出来た速度の方向差の角度で、
その間に出来た白い実線の矢印が加速度の線分となります。
この実線のような極めて短い線分の場合、曲線は限りなく直線に近づく、
という幾何学の基本をここで思い出しましょう。
これはすなわち、弧であれ直線であれ、極めて短いなら同じに扱える、という事です。
となると、加速度を表す短いベクトルは、
円弧の弧と考える事が可能です。
ならば、この部分は二つの速度ベクトルを半径(r)とする
円弧である、と見なせる事になります。
となると、さっそくラジアンの出番ですぜ。
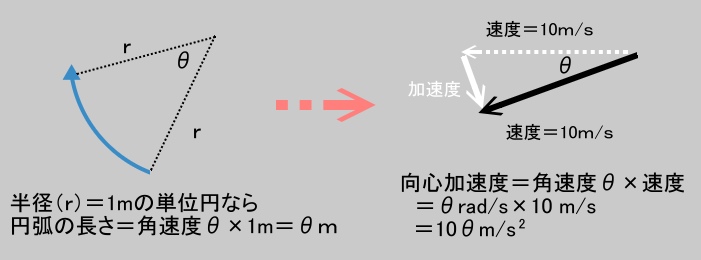
こういうことですね。
ただし、今回は重力加速度の強さを決めてませんし、
引力の重心点(次回登場予定)までの距離も不明なので、
角速度を求めることができませんから、わかるのはここまで、となります。
とりあえず、向心加速度を求める式がわかった、というとこまでです。
確認すると、極小時間dt の変化量なので、加速度の直線部分を円弧と見なしていいなら、
角θは物体がその間に動いた角速度(ω)であり、物体の速度は半径(r)となります。
これをラジアン単位でθrad/秒(s)とするなら、
向心加速度=角速度θrad/秒(s)×速度m/s
が成立します。
これが向心加速度を求める式です。
そして、先にも書いたようにrad は無次元の量ですから、
計算の結果、その単位はm/ssとなり、
まさに加速度の次元の単位になって出てきます。
…こういったように理論が正しければ、矛盾無く単位が揃ってゆく、
という辺りがニュートン力学の凄みであり、ここら辺りは
極めて堅牢な理論体系だなあ、という印象を受けますね。
当然、加速度ですから、ここでは質量は必要とされません。
この加速度を、それぞれの質量に掛け算することで、力(F)になるのです
さて、ここまで理解できたよ、というあなたには、
その先の扉を開けておきませう(笑)。
ここで使った微小時間dt の間の速度(dV)=10m/s、
実はこれ自身も円運動における弧になってます。
よって、これもまた別のラジアンの計算の対象になるのです。
図にするとこうですね。
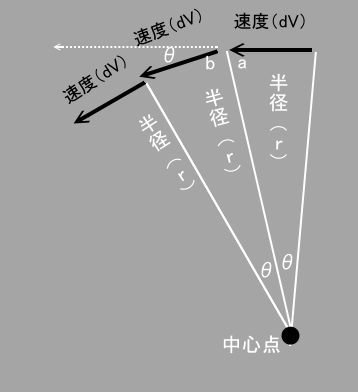
図のように次々と方向が変化する微小速度(dV)=10m/sのベクトルを
どんどんつなげて行くと、最終的にこれは円になります。
となると、ベクトルの量端から円の中心点を結ぶと
これは円運動の半径になるはずです。
はい、またも円弧が見えて来ましたね(笑)。
ラジアンを使うと以下の式が成り立ちます。
速度m/秒(s)=角速度θrad/秒(s)×円運動の半径m
ここでも、単位が速度のm/sになるのに注意しといてください。
が、これは速度を求める式であり、向心加速度を
ここから知ることはできません。
が、先に向心加速度を求めた最初の式を使って、
円運動の半径と角速度から向心加速度を求める式を
作り出すことが可能です。
向心加速度=θrad/秒(s)×速度m/秒(s)
の最後の速度は、
速度m/秒(s)=θrad/秒(s)×円運動の半径m
という今回の式から、
角速度×円運動の半径に等しい、とわかります。
よって、
向心加速度=θrad/秒(s)×θrad/秒(s)×円運動の半径m
といった向心加速度をもとめる式も成立します。
よって向心加速度を求める式は、複数存在し、
通常は、以下の二つが使われることになります。

ちなみに、加速度の向き、力のは向きは、
先に書いたように常に物体に垂直方向ですから、
円運動の半径と同じ向きになります。
ここで最初に見た加速度の円弧の角速度θと、
次に見た円運動の中心角速度θは同じ角度ですから、
どちらの角速度を使っても構いません。

この点の証明も説明しておきましょう。
実は話は簡単で、上の図で角a+b+θ=180度というのが、
一番上の速度と慣性の方向が成す直線に対しても、
そして下側の半径の造る二等辺三角形に関しても成立します。
つまり、どちらの角も、θ=180-a+b ですから、これは同じ角度なのです。
さて、これで角速度、向心加速度、向心力という
円運動の要素が大筋で揃いました。
ここで、あれ?運動量は?と思われた方、するどい。
これは角運動量というものがあり、
質量(m)×運動の半径(r)×速度(V)=角運動量
で求める事ができます。
ただし、これの理論的な説明はちょっと面倒なので、
ここでは、とりあえず、この式で計算は可能なのだ、
という事で終わりとさせてください…。
はい、という感じで、円運動の基礎はだいたい終了です。
もっとも、ここからが大変なので、
あくまで入り口までですが、それでも夕撃旅団の記事を読むくらいなら、
これで十分だと思います。
さて、後は重力と重心と、そしていよいよエネルギーと仕事で、
この迷走しつつある連載も終了です。
BACK