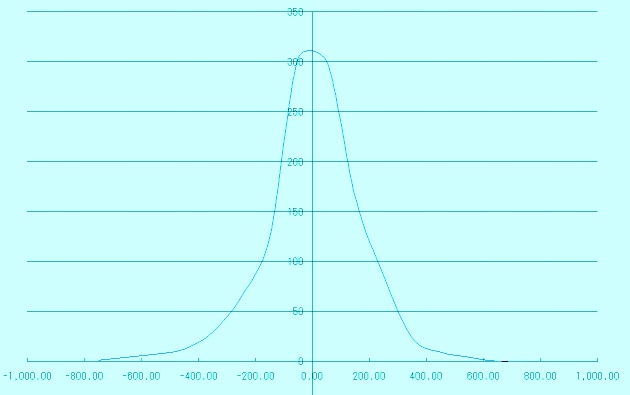
さて乱数集団の種類を判別するためには、その特徴を見つけなくてはなりませぬ。
それは平均値、標準偏差、そして分布の三つの要素で判別されます。
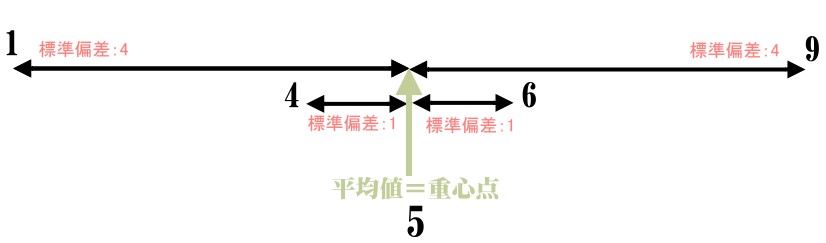
■乱数集団の重心点(中心点)はどこか(=平均値)
■乱数集団がどの程度の広がりを持つか(=標準偏差)
■乱数集団内の各数値はどこにどれだけ固まっているのか(=分布)
この3つが分かれば、ほぼその乱数の集団の特徴がわかります。
よって正規乱数かどうかを判別し、理解するには
まずは上の3つの条件を理解しなくてはなりませぬ。
■平均値
説明不要かとも思いますが、一応、基本となる計算式だけは書いておきます。
こういうの書いとくと、何か頭良さそうに見えますし(笑)。
集団n内の数値の量=N
集団内の数値=n1、n2、n3…nN
(N個の数の集団nだからその最後の数をnNとする)
平均値=(n1+n2+n3…+nN)÷N
■標準偏差
お次は標準偏差。「偏差」の「標準」ですから、まずは「偏差」とは何?という点から。
偏差は平均値から任意の数値nまでとの差(距離)です。
偏差=n - 平均値
平均値が「5」の集団における「10」の偏差は10-5=5で「5」。
同じく「1」の偏差は1-5=-4となるので「-4」。
これは集団内の数値が、平均値からどれだけ離れてるかを求めた数字で、
引き算で計算できます。ここまでは問題なし。
となると、この偏差の数値を見れば、その乱数集団が、
どの程度の広がり(最低&最大値)を持つかが分かります。
が、なにせ乱数ですから、最低と最大の値は、他の数値からとんでもない
距離を持つ数値になってる事があります。
例えば集団の99%以上の数値が-10〜10の間に入ってるのに、
最大値=60,最低値=-50といった偏った数字になってる乱数集団です。
この時、この集団の広がりを最低-50から最大60まで、とするのはさすがに無理があります。
そこで標準偏差という考え方が出て来るのです。
ここでまた平均値が出てきます。
多少、特異な数字があっても、偏差の数字を平均化してしまえば、
大よそ集団の特徴を示す偏差が得られるはずです。
が、発想は正しいのですが、実はこれが単純には計算できません。
これは具体例で説明した方が速いでしょう。
-3、-2、-1、0、1、2、3
この集団の平均値は0、それぞれの数値の値がそのまま偏差となりますから
最大で3,最小で-3の広がりをもつ集団です。
ところがこの集団の平均値は0ですから、偏差の平均もまた0、集団としての広がりは全く無い事に。
これは極端な例ですが、平均値以下をマイナスとして表す場合、どうしても似たような問題が生じます。
このため以下の数式で求める“標準偏差”を利用します。