では正規分布乱数の特徴を見て置きましょう。
ちなみにこれは発見者であるガウスの名をとってガウス分布とも呼ばれます。
ただしこれを厳密に説明するには
確率密度関数(グラフの面積(積分)から求める確率)
の理解と微積分の極北、という展開が必要なんですが、
そんなの書いても誰も読まないし
残念ながら私自身、人に説明できるほど理解できていませぬ。
今回はとりあえず、その結論だけ頂いてしまえば問題ないので、
それでゆく事にします(手抜き)。
乱数集団の正規分布では、以下の特徴が必ず存在します。
よってこれらが観察されたら、それは正規分布の乱数であり、
数学的な考察の対象になる、と思ってください。
■正規分布の乱数集団では、
●平均値から標準偏差未満の差(距離)以内の値に
集団全体の67.8%が含まれる。
●同じく標準偏差×2未満までの差(距離)以内の値に
集団全体の95.3%までが含まれる。
●同じく標準偏差×3未満までの差(距離)以内の値に
集団全体の99.7%までが含まれる。
よって標準偏差3倍以上の差を持つ数値の発生確率は、
全体の0.3%以下、極めて少量となる。
つまり平均値からの標準偏差の距離で見ると、
最大3倍までの幅に、ほぼ全ての乱数が収まってしまう、という事です。
これらを分布のグラフにすると以下のようになります。
表計算ソフトのエクセルで発生させた2000個の乱数集団で前後の値の比をとり、その数を調べたものです。
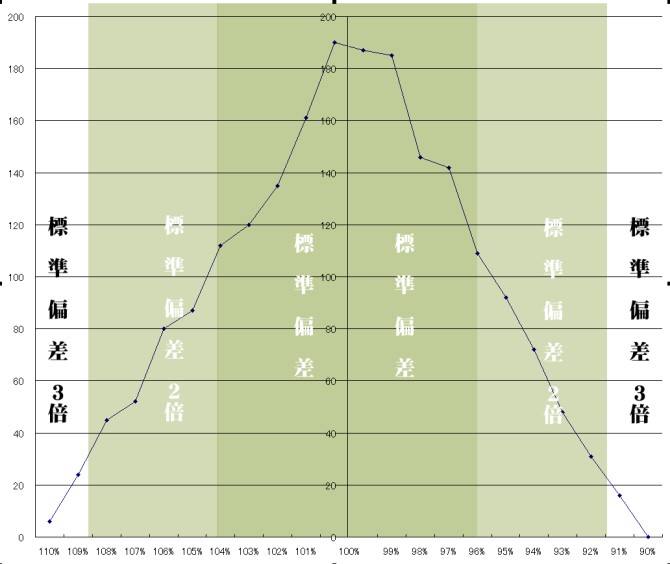
ホントはもっとキレイな釣鐘型グラフになるはずなんですが(笑)、
それでもとりあえず中心値の平均値(集団の重心点)付近に数値が集中しているのが見て取れます。
逆にそこから遠ざかるにつれて、急激に個数が減って行くのが見て取れるでしょう。
今回のデータは平均値100%、標準偏差4.3%の集団で、以下のような分布でした。
標準偏差未満の値 69.2%、
標準偏差2倍未満の値 93.6%
標準偏3倍未満差内 100%
ほぼ正規分布と見なしていいでしょう。
ただし理論値では0.3%はこの枠外に出るハズなんですが、それが無く、
標準偏差から3倍以内に100%と収まってしまっています。
これは極めて行儀の良い乱数であり、逆に言えばここら辺りが人工乱数の限界で、
本来なら生ずるはずの異分子、イレギュラーが生じないのです。
今ではもう少し高度な乱数を生じさせるアルゴリズムなどもありますが、
それでも完全とは言えないというか、そもそも完全な乱数なのかを確認する手段がありませぬ。
よって、これらの乱数を使って実在の現象をシミュレーションすると、間違いなく誤差が生じます。
当然、それは株式の価格変動でも同じことが言えます。皆さん、なぜか無視してますけどね。
この点は要注意だと思ってください。
さて、では現実の乱数、日経平均株価のデータを使って現実世界の現象を検証してみましょう。
NEXT