■それは予測できない

では日経平均株価の変動率はホントに乱数になってるだろうか。
これを1000回分の変動率データで確認しよう。

ただし1000回分のデータをここに並べても読みにくいし、
実際誰も読まないと思うので、ここでは結論だけを述べて行く。
先に書いたように日経平均株価データは誰でも入手する事ができるから、問題はないだろう。

とりあえずそれには、先のページで見た

●n番目の数値とその倍数の位置にある数値を抽出、並べた時に、
なんらかの周期性が発見できるか。

●各数字の出現確率は計算で求められる予測値と近似するか

の2点を確認すればいいだけだ。さっそく見てみよう。



まず最初のn番目の抽出だが、
正確を期すなら複数の数値での確認が望ましい。
とりあえずn=2、n=3で見てみよう。

まずn=2、つまり一つおきに変動率の数字を抽出した場合、最初の20回分を見ると

100.7%、99.6%、101.0%、102.6%、104.0%、97.8%、97.6%、99.2%、99.3%、100.3%、
99.4%、100.5%、101.3%、99.3%、101.1%、99.8%、100.8%、100.3%、100.0%、100.4%

となる。
100.3と99.3が2回出てくるものの、それ以外の数字に重複はなく、
その2つもまるでバラバラに登場している。
周期性は無いと言っていいが、もう少し長い期間でも確認する必要があるだろう。
その場合はグラフで見たほうが早い。
もし周期性があるなら、三角関数のサイン、コサインカーブのような
周期的な波形のグラフになるはずだ。

n=2


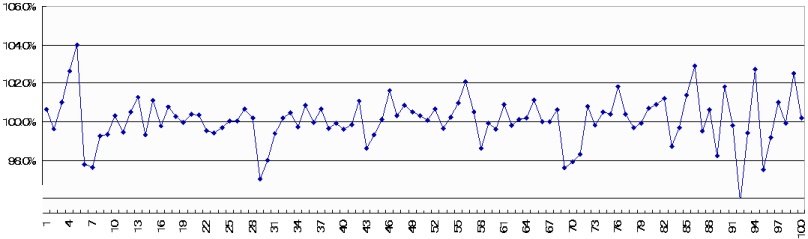
とりあえず抽出100番目の数字までをグラフにするとこうなる。
とにかくグラフを見て判断するしかないのだが、
100％を境に上下に常に振幅してるものの、
おなじ形が正確に繰り返される、という周期性は見られない。

何箇所かで唐突に大きな変動があるのでこれを目印に、
40〜80といった長期の周期での繰り返しを探して見るが、
それでも厳密な繰り返周期は確認できない。
つまり周期性は無い、と判断して問題ないだろう。

ちなみに、あまりに大きくなるのでここでは掲載しないが、
800回までのグラフでも同様だった。
それ以上に大きな幅での周期が無い、とは断言できないが、
今回は1000桁で区切る、というのが前提条件だから、
そんな大きな周期があってもほぼ無意味となる。
よって無視してよい。

さらに他の数字の場合のグラフも上げておこう。

n=3


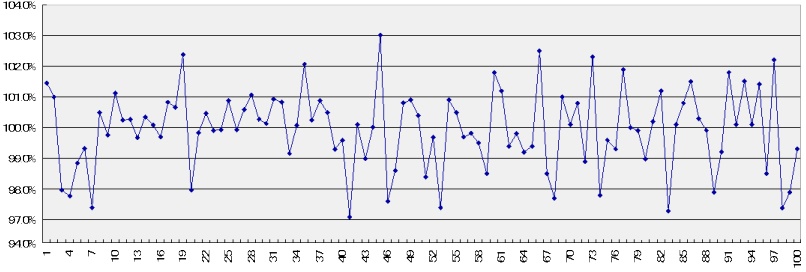
これも基本は同じだ。
100％を挟んで小刻みな動きが繰り返されている。
たまに同じような形が出現するものの、規則性はないし、
実際、同じ波形が正確に繰り返されてるのも確認できない。

周期性はないと見ていいだろう。

では、出現率の確認の方はどうだろうか。
だがサイコロと違って、株価は予め出る数の目が決まってるわけではない。
よって、どうやって値を決めて理論上の出現率を求めるのかを
最初に考えなくてはいけない。

後で見るように株価の変動率の平均値ははキレイに100%（＝変動なし）となる。
ここからプラス値（>100%）とマイナス値（<100%）の出現率は
それぞれ1/2、50%の出現確率とならないと、一定の未来予測が成立してしまう。
（例えばプラス値（>100%）が70%なら一定の時点までにプラスのでる回数の方が圧倒的に多いと判る）
すなわちコイントスと同じように、裏か表のどちらかが
1/2の確率で出る値の集団でなければ乱数ではない。
よって両者の出現率を確認すればいい。その結果は以下の通りだ。

プラス値	マイナス値
510回（52.6％）	461回（47.4％）

理論値の50％に対し両者の誤差は
プラス値　50÷52.6＝95.1％　すなわち4.9％、
マイナス値　47.4÷50＝94.8％　すなち5.2％

ギリギリの数字ではあるが、ほぼ理論上の予測値から誤差の範囲と見ていいだろう。


以上から、日経平均株価の価格変動率は乱数である、と見てよいだろう。
すなわち、力学のように関数の数式を使って株価の未来予測を行う事は一切できない。

が、数学の発展というのは大したもので、実は乱数にも関数的な分析を持ち込む、
それどころか微積分までやってしまう手段が開発されている。

だが、その点を考えるには、株価の変動率の乱数を
もう少し詳しく見ておかなくてはいけない。
乱数というのは、単純に一種類だけではないからだ。

今回のお話はここまで。ではまた次回。


BACK