仭懍搙偲埑椡
傑偢偼崱夞偺儔儉僕僃僢僩偵僄儞僕儞偺峔憿偐傜妋擣偟傑偡丅
幨恀偱偼偙傫側姶偠偵僈儔儞摲偱丄
拝壩晹暘偲擱從晹傪偁傞掱搙墴偝偊崬傓僷乕僣偑拞偵尒偊傞偩偗偱偡丅

柧傜偐偵偙傟偼僸儔乕偺僿儕偵巊傢傟偰偄偨儔儉僕僃僢僩偺僐僺乕偱偡丅
愝寁恾儗儀儖偺僐僺乕側偺偐丄幨恀偱尒偨偩偗側偺偐偼敾傝傑偣傫偑丄丄
摨偠峔憿側偺偼娫堘偄偁傝傑偣傫丅
偱傕偭偰僸儔乕偺儔儉僕僃僢僩偺尨宆偲偄傢傟偰傞偺偑丄偙傟偵側傝傑偡丅
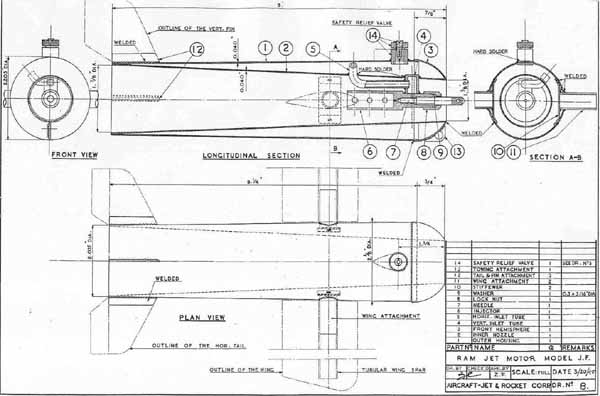
慡偔摨堦偱偼側偄偺偱偡偑丄婎杮峔憿偼摨偠偱偡丅
偲傝偁偊偢丄偙偺恾柺傪婎弨偵峫偊偰傒傑偟傚偆丅
僷僀僾晹暘傪僩儗乕僗偟偰傒傞偲偙傫側姶偠偱丄
嬻婥偺擖傝岥偲擱從晹偺捈宯偺斾偼偍偍傛偦1丗1.3偱偡丅
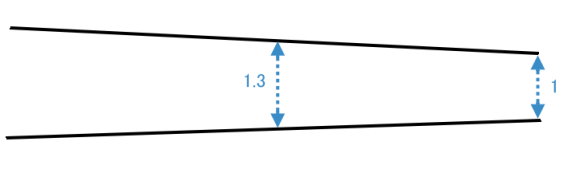
幚嵺偺悺朄偼帤偑彫偝偔偰撉傒庢傟側偄偺偱偡偑丄
尰暔傪尒傞尷傝丄偣偄偤偄20cm偱偟偨丅
偙偙偱偼傗傗梋桾傪尒偰擖傝岥偺捈宯30cm丄
擱從晹偵偍偗傞捈宯39cm偲偟偰偍偒傑偟傚偆丅
屻偱尒傞傛偆偵丄幚偼偙偺戝偒偝丄偦傟傎偳堄枴偑柍偄傫偱偡偗偳偹乮徫乯丅
偙偙偱儔儉僕僃僢僩偼梼柺忋偺徴寕攇偺栤戣偑惗偠側偄儗儀儖偺崅懍丄
偞偭偲帪懍720噏丄昩懍200m偱旘峴偟偰傞偲壖掕偟傑偡丅
偊偊丄寁嶼偑妝偩偐傜偱偡乮徫乯丅
偮偄偱偵丄棳懱偑嶌傝弌偡憌棳傗塓偲偄偭偨擄栤傕柍帇偟傑偡丅
偁傞掱搙偺嬤帡抣傪摼傞偩偗側傜丄栤戣側偄偱偟傚偆丅
偙偆偄偭偨峀偑傝傪傕偭偨娗偺拞偱丄
擖傝岥偐傜擖偭偨婥懱偺棳懍偼丄
恑傓偵楢傟偰懍搙偑掅壓偡傞偺偑幚尡側偳偱妋偐傔傟偰偄傑偡丅
偦偟偰摨帪偵埑椡偑忋偑傞偺偱偡丅
偙偺埑椡忋徃傪棙梡偟偨偺偑儀儖僰乕僀偺掕棟傪巊偭偨儔儉僕僃僢僩偱偡偑丄
側傫偱偦傫側帠偵側傞偺偐傪丄弴傪捛偭偰尒偰偍偒傑偡丅
偦偙偐傜嵟廔揑偵丄偙偺峔憿偱僕僃僢僩僄儞僕儞偲偟偰巊偊傞傎偳偺
埑弅偑峴側傢傟傞偺偐傕峫偊偰傒傑偟傚偆丅
傑偢偼娙扨偵棟夝偱偒傞懍搙偺掅壓偺尨場偐傜丅
偙偺儔儉僕僃僢僩偺娗偵椺偺埑弅偝傟側偄棟憐婥懱偑棳擖偡傞偙偲傪峫偊傑偡丅
30cm偺擖傝岥偺堦掕柺愊偐傜偳傟偩偗偺懱愊偑棳傟崬傓偐偼
棳懱偺懍搙偲宱夁帪娫偵傛傝傑偡丅
偙偺30cm偺擖傝岥偺柺愊偼丄0.3m亊0.3m亊3.14亖0.071暯曽m偱偡偐傜丄
戝婥偑昩懍200m偱棳擖偡傞側傜丄1昩娫偵偮偒
0.071暯曽m亊200m/s亊1s亖14.13棫曽m
偺棳擖検偲偄偆寁嶼偑惉傝棫偪傑偡丅偡側傢偪丄
抐柺愊亊棳懍亊宱夁帪娫亖抐柺傪捠夁偟偨婥懱偺憤懱愊
偲偄偆寁嶼幃偱偡偹丅
偙傟偼棟憐婥懱偱偡偐傜丄摨偠懱愊側傜忢偵摨偠枾搙丄
傛偭偰摨幙検偱偁傝丄偳傫側椡妛揑側忦審壓偱傕忢偵堦掕偲側傝傑偡丅
偮傑傝偙偺寁嶼幃偼晛曊揑偵偁傜備傞忦審偵揔梡偱偒傞傢偗偱偡丅
乮枾搙偺崁栚傪僉僠儞偲妡偗嶼偡傟偽棟憐婥懱偱側偔偰傕惉傝棫偮乯
偲側傞偲丄偙偺幃傪曄宍偟偰丄棳懱偺懍搙傪媮傔傞帠偑偱偒傑偡丅
棳懍亖抐柺傪捠夁偟偨婥懱偺憤懱愊亐抐柺愊亐宱夁帪娫
偱偡偹丅
偙偙偐傜丄抐柺愊偑彫偝偔側傞偲棳懍偑懍偔側傞丄
媡偵戝偒偔側傞偲棳懍偑抶偔側傞偲偄偆偺偑敾傝傑偡丅
偙傟傪尦偵丄崱夞偺儔儉僕僃僢僩僄儞僕儞偺拝壩揰丄1.3攞偺戝偒偝偲側傞
捈宎39cm亖0.39m偱偺婥懱偺棳懍傪峫偊傞偲丄
抐柺愊亖0.39亊0.39亊3.1415亖栺0.12暯曽m丂傛偭偰
棳懍亖14.13棫曽m亐0.12暯曽m亐1倱亖栺118.3m/s
擖傝岥偺昩懍200m偵斾傋傞偲丄偐側傝抶偔側傞偺偑敾傝傑偡丅
偱偼丄師偵埑椡偺忋徃偵偮偄偰丅
偙偪傜偼桳柤側儀儖僰乕僀偺掕棟偺埵抲僄僱儖僊乕偑柍偄忬懺丄
偮傑傝悈暯偺棳傟偩偗傪峫偊傞幃傪巊偄傑偡丅
儀儖僰乕僀偺幃偺寁嶼曽朄偼挿偔側傞偺偱丄偙偙偱偼寢榑偩偗彂偄偰偟傑偆偲丄
棟憐婥懱偑擲惈傪柍帇偱偒傞忬懺乮暻偵憌棳傪偮偔傜側偄乯
悈暯偺棳傟偺拞偵偁傞偲壖掕偟偨帪丄
棳懱偺埑椡+1/2亊棳懱懍搙亊棳懱懍搙亊棳懱枾搙亖堦掕乮師尦偼埑椡偱扨埵P/僷僗僇儖偵側傞乯
偲偄偆幃偑惉棫偟傑偡乮崱夞偼棟憐婥懱偲偟偨偑枾搙曄壔偵傕懳墳偼偱偒傞乯丅
偙偺幃偼丄奜晹偐傜怴偨偵僄僱儖僊乕傪庴偗傞偙偲偑柍偄棳傟偱偼丄
埑椡偲丄1/2亊懍搙偺2忔亊枾搙偺懌偟嶼偺寢壥偼忢偵堦掕偲側傞丄偲偄偆帠傪堄枴偟傑偡丅
堦庬偺僄僱儖僊乕曐懚偺朄懃偩偲峫偊偰偔偩偝偄丅
偙偙偱怴偨偵棳懱枾搙丄偲偄偆崁栚偑搊応偟傑偟偨偑丄偙傟偼椺偺棟憐婥懱偺枾搙偱偡丅
尰幚偺僄儞僕儞偺弌椡傪峫偊傞偺偱偡偐傜丄昗弨戝婥偺
抧忋晅嬤偺枾搙傪嵦梡偟偰偍偒傑偟傚偆丅偙傟偼栺1.225kg/暯曽m偱偡丅
忢偵堦掕側偺偱偡偐傜丄崱夞偺忦審偺応崌丄
擖傝岥偺埑椡+1/2亊200m/s亊200m/s亊1.225kg暯曽m
丂丂丂丂丂丂丂丂丂亖拝壩揰偺埑椡+1/2亊118.3m/s亊118.3m/s亊1.225kg暯曽m
偲偄偆幃偑惉傝棫偪傑偡丅
偙偙偱擖岥偺埑椡偑傢偐傟偽丄拝壩揰偺埑椡傪媮傔傞帠偑偱偒傞丄偲偄偆偺偼丄
偙偙傑偱僈儅儞偟偰撉傫偱偒偨奆偝傫側傜婥偑晅偔偱偟傚偆乮徫乯丅
偱偼丄擖傝岥偺婥埑偼偄偐傎偳偐丅
偙偺帪丄嬻婥偼慡偔塣摦傪偟偰偍傜偢丄旘傫偱偒偨儔儉僕僃僢僩僄儞僕儞偵
堦曽揑偵姫偒崬傑傟丄庢傝崬傑傟傞偺偩丄偲偄偆揰偵拲堄偑梫傝傑偡丅
偮傑傝戝婥偺帩偮塣摦僄僱儖僊乕偼僛儘偱丄偟偨偑偭偰椡妛揑側椡傕偐偐偭偰偄傑偣傫丅
偲側傞偲偙偺戝婥偺帩偮埑椡偼戝婥埑偺傒丄偲偄偆帠偱偡偹丅
僯儏乕僩儞椡妛偵偍偗傞埑椡偺扨埵偼N乮僯儏乕僩儞乯/暯曽m亖僷僗僇儖乮P乯偱丄
抧忋偵偍偗傞昗弨婥埑偼101325P丅
傛偭偰忋偺幃偺嵍忋晹暘丄擖傝岥晅嬤偺悢抣寁嶼偺寢壥偼丄
101325亄1/2亊200亊200亊1.225亖125825僷僗僇儖乮p乯
傛偭偰
125825亖拝壩揰偺埑椡+1/2亊118.3m/s亊118.3m/s
亖125825亖拝壩揰偺埑椡+8578
亖125825-8578亖拝壩揰偺埑椡
亖117247p亖拝壩揰偺埑椡
偲偄偆帠偵側傝傑偡丅擖傝岥偱偺埑椡偼
昗弨婥埑101325偱偟偐偨傜丄埑椡嵎偼
101325亐117247亖栺1.16攞
偲偄偆帠偵側傝丄偙傟偼崱夞偺儔儉僕僃僢僩偺峔憿偱偼丄
帪懍720噏偩偲丄僄儞僕儞偺拝壩揰偵偍偄偰
昗弨戝婥埑偺1.16攞偺埑椡偵偟偐側傜側偄丄偲偄偆帠傪堄枴偟傑偡丅
偙傟偼偣偄偤偄丄壛埑悊斞婍偑偐偗傞埑椡儗儀儖偱偡偐傜丄
嵟掅偱傕8乣10攞慜屻偺埑弅斾偑昁梫偲巚傢傟傞
僕僃僢僩僄儞僕儞偲偟偰巊偆偵偼偪傚偭偲柍棟偑偁傞丄偲峫偊偞傞傪摼傑偣傫丅
晛捠偵峫偊傞側傜丄挻壒懍偱傇傫夞偟偰丄僄儞僕儞僫僙儖偺慜曽偵偱偒傞
徴寕攇攚屻偺壛埑嬻婥傪巊偆偮傕傝偩偭偨偺偱偼側偄偐丄偲巚傢傟傑偡丅
壒懍埲壓偺偱偺旘峴偵偼揔偟偰側偄峔憿偱偟傚偆丅
嶲峫傑偱偵丄擖傝岥傪嫹偔偡傞丄偁傞偄偼摲懱傪懢偔偡傞側偳偟偰丄
抐柺愊偺斾棪傪曄偊傞偲偳偆側傞偐丄傪彂偒弌偟偰偍偒傑偟傚偆丅
1丗1.5亖1.19攞
1丗2亖1.23攞
1丗3亖1.24攞
1丗4亖1.24攞
幚偼4攞埲忋偺戝偒偝偵側傞偲傎偲傫偳堄枴偑側偄丄偲偄偆偺偑敾傝傑偡丅
帪懍720噏慜屻偱偼丄偲偰傕廫暘側埑弅棪偼弌側偄丄偲偄偆帠偱偡丅
偪側傒偵丄徴寕攇偑惗偠傞捈慜乮庡梼偵偼婛偵悅捈徴寕攇偑弌傞乯
帪懍1080噏丄昩懍300m傑偱壛懍偟偰傕丄
1丗1.3攞乮崱夞偺椺乯亖1.35攞
1丗1.5攞亖1.44攞
1丗2亖1.51攞
1丗3亖1.54攞
1丗4亖1.54攞
偲傗偼傝偙偺傑傑偱偼丄偲偰傕僕僃僢僩僄儞僕儞偵偼巊偊側偝偦偆偱偡丅
挻壒懍徴寕攇偺攚屻偵偁傞埑弅嬻婥偺棙梡傪偁偒傜傔傞側傜丄
摏撪傪懡抜幃偵偟偰丄擇廳埑弅傪偐偗傞丄偲偄偭偨岺晇偑偄傞傛偆偵巚偄傑偡丅
乮偨偩偟丄偆傑偔峴偔偐偼曐忈偟傑偣傫乮徫乯乯
偲偄偭偨姶偠偱丄傗偼傝挻壒懍旘峴傪幪偰偨儔儉僕僃僢僩偼丄
婎杮揑偵尩偟偄丄偲偄偆帠偵側傞傛偆偵巚偄傑偡丅
BACK


