最初に、今回行う測定誤差距離の推定方法を説明します。
まず測距儀で距離を測るには相手を目視で捕らえ、
その角度を読み取る必要がある、というのはすでに説明しました。
この時、その角度に前ページで説明した「人間の分解能力限界」以下の
ズレがあっても、人間には読み取る事ができません。
それは必ず誤差として残ります。
では、それはどれくらいの大きさなのか。
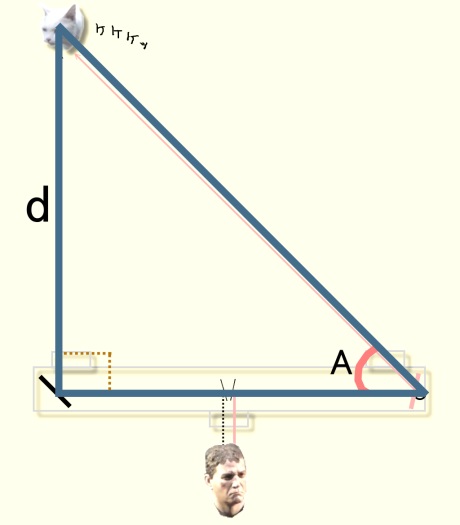
ここで前に使った図を再度見ておきましょう。
この図で∠Aを決定する「角度の変わるミラー」
が最小で0.5'ズレても、人間には読み取れないわけです。
それは必ず誤差として残り、
それ以上、観測の精度を上げる事はできません。
なので、それが測距儀による主砲照準の精度の限界となります。
では具体的に、それはどの程度の数字なのか。
これを検証するには、まず人間の読み取り誤差を決める必要があります。
これは最小で0.5′、平均で1′でした。
とりあえず最小の理論値という話ですから、今回は0.5′で考えて見ます。
これが∠Aの測定において、避けられない角度誤差と考えられます。
ただし、レンズを明るくするにはそれなりの技術が必要で、
当時の日本の光学技術ではかなり厳しいものがありました。
その焦点距離(図面読み取りで400mm前後)を考えても、
決して視野は明るくないはずで、
とても人間の裸眼の限界値に迫る事はできないでしょう。
実際は理論値の半分以下だったと思われますので、
この点は覚えて置いてください。
次に三角形の底辺にあたる大和級の測距儀の有効基線長は
前ページの通り15.7m×30=471m=0.471㎞
目標までの距離(d)は、一般的な戦艦の砲撃戦距離として
20、30、35、40㎞の場合を考えましょう。
この条件で、読み取りの角度誤差1/120度=0.5′(0.5分)が生じた場合、
どの程度の距離の差が生じるのか、という事です。
その距離が避けられない観測上の誤差となるからですね。
上の図で考る場合、底辺0.471㎞、距離(d)が20、30、35、40㎞の
それぞれの三角形において、
∠Aの角度が1′ずれた場合、距離(d)がどれだけ変わるか、という事です。
となると、まず、∠Aの角度を求める必要がありますが、
今回はTan A が各距離÷有効基線長0.471で求められるので、
そこから角度を逆算する三角関数、アークタンジェント(Atan)を使います。
で、それぞれの距離のときの、∠Aの角度は以下の通り。
20㎞ 1.547度
30㎞ 1.555度
35㎞ 1.557度
40km 1.559度
そもそもこんな角度が読み取れるのか、という感じですが(笑)、
そこに誤差として避けられない1/120度=0.5′=約0.00833度を足し算します。
後はその角度の数字に対するtanの値を求め、再度、最初に見た
距離(d)=tanA×測距儀の長さ
に当てはめて見ましょう。結果は
20㎞の時 20.12㎞
30㎞の時 30.28㎞
35㎞の時 35.38㎞
40㎞の時 40.5km
両者の差が避けられない誤差の距離ですから、
引き算をすれば、
20㎞の時 約120m
30㎞の時 約280m
35㎞の時 約380m
40㎞の時 約500m
となります。
人間の目で観測する限り、
これ以上の精度で対象までの距離を測る事ができない、という事ですね。
確認して置くと、これは日本海軍最大だった大和級のもので、
しかも晴天で十分な明るさがある、という前提条件があります。
なので天候によってはさらに悪化し、
他の戦艦、巡洋艦では、晴天ですらより劣った数字になるわけです。
これは最大の分解能力、どれだけの長さまで識別できるか、
という事でもありますから、例えば40㎞の時には距離は
事実上、500m単位でしか計測できない、という事です。
それ以下の距離は測りようがありません。
(目盛りでは読み取れるが全くもって正確ではない)
これは1cm単位の目盛りしかない定規でmm単位の長さを測れ、
というような話になってきます。
先に見たように放物線で弾が飛んでゆく戦艦の砲撃戦では、
まさに点に向けて砲弾を命中させる必要がありますから、
正確な距離の数字は何より重要なのに、それを得る事は
人間の目を使っている限り、できないのです。
最大500mもズレたら、どう考えても当たるか当たらないかは運になります。
ちなみに通常、戦艦の主砲の射撃は最初の着弾の水柱の位置を見て、
20m奥、いや手前、という感じに砲撃を調整して行き、命中弾を出します。
が、着弾がどれだけズレたのかを知るのに、
その正確な距離がわからないんじゃ調整のしようがありません。
そもそも水平線を越えてしまう25㎞以上の相手には
砲弾が手前に落ちたのか、行過ぎたのかもわからん、
というのはまた後で見て行きます。
どれほど砲撃が優秀でも、そもそも指示された目標までの距離が
これだけ違ってしまっていたら、当たる訳がないと考えていいでしょう。
繰り返しますが、命中するかどうかは、完全に運となります。
で、ここら辺りの問題を一気に解決してしまうのが
射撃管制レーダーなんですが。
とりあえず、
測距儀で計測した距離の数字で照準を決めてやる長距離砲撃は
いろいろ厳しいから、やめたほうがええよ
が今回の結論となるわけです(笑)。
少なくとも、レーダー無しで35㎞以上の遠距離砲撃なんて、
弾をドブに捨てるようなものとなるでしょう。
BACK