さて、ここまで見てきた、物体に複数の力が加わるケースは、
すべて同一直線上で力が作用する、というものばかりでした。
つまり、直線の世界、一次元の空間での力のやり取りのみです。
が、世の中がそんなに単純なはずは無く(笑)、
例えば水平飛行中に発射された対空ミサイルを考えてみましょう。
この時、ミサイルには水平方向にロケットモーター(エンジン)の力がかかり、
垂直方向には地球の重力がかかっています。
この両者の力の向きは同一直線上には無く、
垂直に交わる事になりますから、
これは2次元平面における力のやり取りとなります。
(実際は3次元で展開するが、単純化してしまえば2次元でまとまる)
その力の合成はどうなるのか?
少なくとも、これまでのような単純な足し算、引き算ではダメそうです。

ここまでは、こういった一直線状の運動でのみ、力のやり取り、合成を考えてました。
それが一番楽だからですが(笑)、世の中には2次元、3次元の力の向き、
というのは当然あるわけですし、むしろそれが普通です。
今回は、とりあえず2次元、平面で考えられる力の合成までは見ておきましょう。
それ以上はさすがに話がヤヤコシクなり過ぎますしね。
が、こういった問題もグラフで考えると解決できます。
力の合成、と呼ばれる作業を行う事で、
物体にかかる力の大きさ、向きを
正確にに求めることが可能になるのです。
さらにグラフなら2次元の空間はもちろん、
座標を増やせば3次元空間も対応できますからね。
で、力の問題なので、例によって時間を区切る必要があり、
今回もとりあえず1/10秒単位で考えましょう。
話を単純にするため、ミサイルの質量はわずか1kgの
とても計算に向いた兵器だとしてしまいます(笑)。
さらにミサイルの推力、抵抗力も大体ですが、下のグラフの数値とします。
数字を変えても考え方は同じですから、
推力が十分ある、という前提なら、数字は適当でかまいませんので。
ただし、地表付近における重力は常に一定であり、
これは重力加速度 約9.8m/ssから計算できます。
加速度がそれなら、かかる力(F)の大きさは、
力(F)=質量(m)×加速度(a)ですから、
1kgの物体で1秒間に9.8kg・m/ss、1/10秒単位なら0.98kg・m/ssとなります。
重力については、位置エネルギーの話でもう少し詳しく見ますので、
ここでは単純にそういったものだと考えておいてください。

では、グラフの内容の説明を。
■1の座標0の原点にミサイルがある、と考えると、
そこにかかる力はこんな感じに大きく3つに分かれます。
で、エンジン推力と抵抗力は同一直線上の逆向きの力ですから、
今まで通り、単純に足し算でその力を合成できます。
合計は3+(-1)=2kg・m/ssの力ですから、これが前向きに加わった状態が、
■2のグラフとなります。
が、もう一つの力、重力とエンジン推力は同一直線上には無く、
両者は垂直に交わってしまっています。
この力の合成はどうすりゃいいの、というのを少し考えてみましょう。
ここでまず、運動法則を思い出してください。
●力を加えるのは一度にやってもいいし、複数回に分けてもいい。
というルールがありました。
同じ量の力を一度に加えても、複数回に分割して後から合計しても
その結果は同じ事になるよ、という意味です。
よって、力の合成を以下のように考えてみましょう。
まずは単純に同一直線状の場合。

■1 まず、最初にエンジン推力が単体で+3kg・m/ssかかったと考えます。
■2 次の瞬間、そこに抵抗力-1kg・m/ssがかかったと考えましょう。
両者は同一直線で逆向きですから、推力は単純に+2kg・m/ssに押し戻されて
そこが合計の推力となります。
これで、二つの力を合成した力の大きさが判るわけです。
実際、3+(-1)=2kg・m/ssで、計算結果とも一致しますね。
ただし計算の都合上、2段階に分けて考えてるのであって、
実際には両者の力は同時に発生してる、
というのは忘れないでください。
さて、同じ考え方で推力と重力も分割、合成してみましょう。
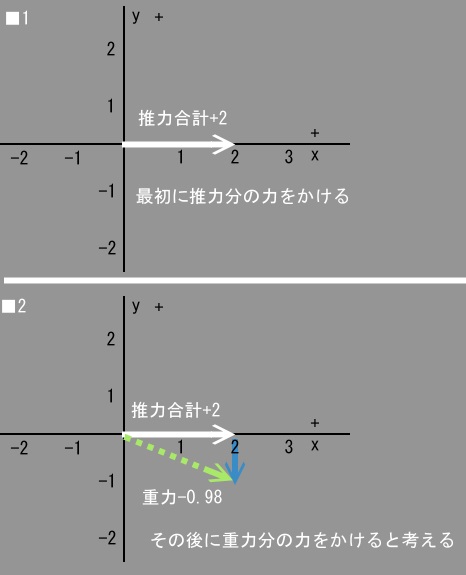
■1 まず上で求めた推力の合計、+2kg・m/ssがミサイルにかかると考えます。
■2 次にそこから下向きの重力、-0.98kg・m/ssがかかると考えます。
この結果、その合成した力の座標は青い矢印の
先端部となりますから、この点とミサイル、つまり原点を結んだ線が
合成された力の大きさと向きであり、これは緑の点線のような矢印となります。
この力が飛行中のミサイルにはかかっているわけです。
その力の大きさを知るには、この直線の長さを測る必要がありますね。
これも考え方は簡単でして、グラフ上の座標から、
計算でその長さを求めてしまう事ができます。
とりあえず、この力をFと名付けておきましょう。
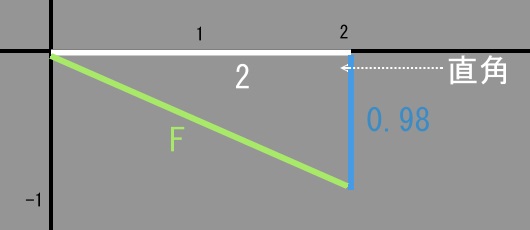
で、上のグラフをよく見ると、こういった直角三角形になってます。
水平飛行するエンジン推力と重力は垂直に交わるのですから、
当然といえば当然ですね。
でもって、さらにこの三角形では2つの辺の長さが判っています。
…はい、その通り、ここでピタゴラス閣下の登場です。
直角三角形の3つの辺の長さでは、
以下の関係が常に成立する、とういうヤツですね。

今回、上のグラフで長さを知りたい力=Fの辺は、
この図ではaの辺に当たる、とういうのはわかりますね。
よって、この力の辺の長さは、
F = √2×2+0.98×0.98=2.2271…
で、約2.23kg・m/ssとなる、というのが計算で求められてしまうのです。
もっとも、毎回こんなに都合よく直角三角形にはなりませんが、
X軸、Y軸どちらかに垂線を引いて、2つの直角三角形に分ける、
といった一工夫で、ここら辺りは乗り切る、等でなんとかなります。
まあ、さらに難解な場合もあるんですが、今回は基礎知識編なので、
これ以上はやりません。
あとは皆さんのガッツでカバーに期待します(手抜き)。
ちなみに、グラフを使わずに、計算式だけで求める場合、
それぞれのX軸とY軸の数字(X、Y)を足し算して座標を出します。
まずは推力。これはY軸(高さ)は0でX軸(距離)は2でしたから
(0、2)
といった形で書きます。
次に重力。これはY軸(高さ)は0.98でX軸(距離)は0、よって
(0.98、0)
となりますね。なので、その計算式は
(0+0.98、2+0)=(0.98、2)が求める座標です。
まあ、グラフを見れば当たり前といえば、当たり前の数字ですが(笑)。
これでX,Yの辺の長さが分かったわけですから、
後は基本的に上と同じくピタゴラスの式で計算するのが
一番分かりやすいでしょう。
が、今回は、これまでの一次元の直線の力と違って、
高さと長さのある2次元の力ですから、
その力の向きが問題になってきます。
従来のようにプラス方向、マイナス方向だけの説明で終わらせるのは無理で、
これはグラフの原点における角度で示すことになります。

が、今回の例は、これまた直角三角形で、
しかも全ての辺の長さがわかってる、という事で計算は一瞬です(笑)。
今回は三角関数、サイン(sin)、コサイン(cos)、タンジェント(tan)を使います。
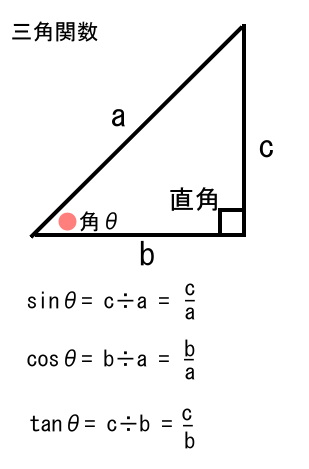
三角関数を簡単に説明しておきましょう。
三角形の全ての内角の合計は必ず180度になります。
でもって直角三角形の場合、直角部の90度は決定済みですから、
あと一つ、上の図で角θ(シータ)の角度が決まれば、
最後の一つの角度も自動的に決まります(=180-90-θ)。
つまり直角以外の2つの角のうち、1つの角度が決まれば、
その直角三角形の形は決定されてしまう、という事です。
となると角θの角度が同じなら、全ての直角三角形は相似、
つまり辺の長さが等しいとは限らないけど、
各辺どうしの長さの比率は常に等しい三角形になります。
比率は割り算で求めますから、図のような割り算によって、
それぞれがサイン(sin)、コサイン(cos)、タンジェント(tan)と呼ばれます。
角θの角度が同じなら、全ての直角三角形において
この3つの比率の数字は等しくなる、というわけです。
逆に言えば、この比率の数字が分かれば、
それに対応する角θの角度は一つしかない、という事です。
そして、この3つの比率の数字一覧とその角度は三角関数表という
チョー便利な表にまとめられているため、
出てきた数字に合う角度をその表から探せば、
一発で角θの角度がわかってしまうのでした。
ついでにキチンと三角形の全ての辺の比を取るなら、
図の式をひっくり返したものも成立するため、
全部で6つの割り算が成立します。
が、通常、上の3つが基本となるので、
とりあえずこれだけを覚えておいてください。
残り3つも本気で戦争をやる場合、使う必要がありますが、
平和を愛する夕撃旅団としては、上の3つだけ
覚えておけば、当面は大丈夫です(笑)。
ちなみに、角θ(シータ)のθ(シータ)は幾何学で角の名前に
よく使われるギリシャ文字であり、空から降ってくる人物ではありません。
角の記号になぜこれが使われるのかよくわかりませんが、
ここでは、世の中の例にならっておきます。
さて、力の向きはどうなるのか、結論を書いてしまいましょう。
とりあえず、再度、グラフを確認しておきます。

せっかく全部の辺の長さが分かっているので、
3つの三角関数の比の数字を全て求めておきます。
図では角に名前を付け忘れましたが、これも角θとしておきましょう。
sinθ= 0.98÷2.23=0.439…
(角θに触れない辺を、直角に触れない辺で割る)
cosθ= 2÷2.23=0.896…
(角θと直角に触れる辺を、直角に触れない辺で割る)
tanθ= 0.98÷2=0.49
(角θに触れない辺を、角θと直角に触れる辺で割る)
後は、出てきた数字を三角関数表と付き合わせるだけです。
今ではネットでもいくらでも見れますから、各自探してみてください。
(アーク(A)計算ができる表計算ソフトがあるなら、それで計算しても可)
ただし、今回の場合、合成した力の大きさ、2.23は四捨五入した数字なので、
それぞれの関数の数字に微妙なズレがでます。
とりあえず、3つの数字が対応する角度の平均値、約26.3度といった
あたりの数字を採用しておきましょう。
これで原点(物体)に対する力の向きがわかりました。
ただし、2次元の力の向きの場合、
座標軸の数字にはいくつかの取り方があります。
360度で全方位表示する、上下180度ずつに分けてプラスマイナスにする、
rad(ラジアン)で示す、などです。
ラジアンはまた後で説明しますので、今回の場合は角度で考えます。
まず、360度表記なら、基準線まで26.3度だけを残した方向ですから、
360-26.3=333.7度。
マイナス表記がありなら、下向きの-26.3度、
というのが力の向きになる、という事です。
はい、これで力を線分と矢印のベクトルで現す、
という説明はおわりです。
とりあえず、一番めんどくさいと思われる話が片付きました。
次回、もう一回だけ、細かいルールを見て、
上手く言ったら微分積分まで片付けてしまいませう。
そこからは、いよいよラストスパートです。
BACK