今回のデータは日経平均株価の終値2000回分、2008年〜2016年2月までを採用してます。
前回の記事同様、毎日の価格の比です(前日終値÷当日終値)。
つまり、前のページで見た“人工乱数”と同じ内容の標本と数量を確保してるわけです。
条件が全く同じなら、それぞれはどんな分布を見せるのか。
さっそくグラフを見てみましょう。
ちなみに日経平均値の比データは平均値100%、標準偏差1.72%となります。
■日経平均終値 上昇率 2008〜2016 標本数2000
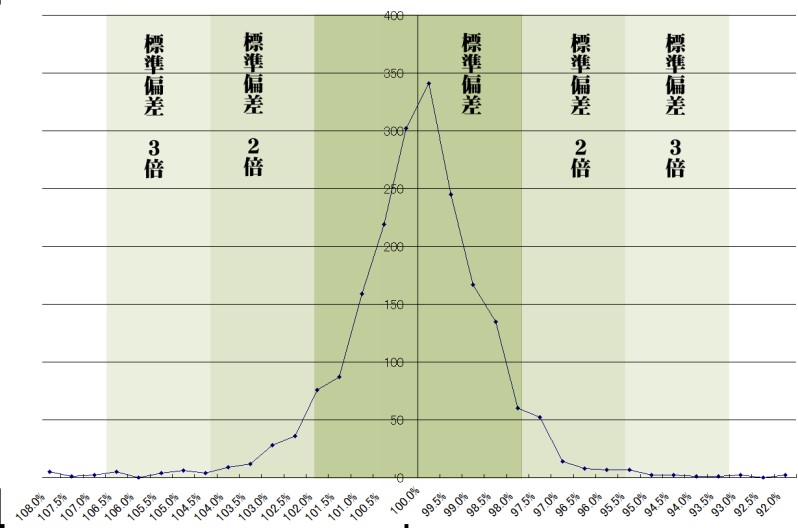
でもって、エクセルの“人工乱数”も再度掲載。
■エクセルによる人工乱数。標本数2000
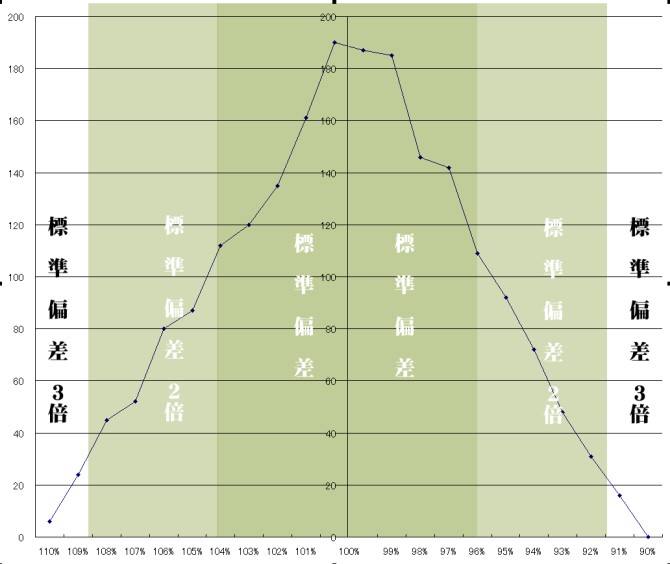
はい、一目でわかるように、全く別物です(笑)。
エクセルの“人工乱数”がダイエットに失敗して体調崩した富士山くらいの形なのに、
日経平均の方は体調万全で東京マラソンに来たマッターホルンのような形状になってます。
平均値の位置で最大量の分布を持つ、という点は共通ですが、
それだけでは、当然、正規分布の証拠にはなりませぬ。
実際、日経平均の方の標準偏差内分布をみると、正規分布の理論値とはかなり異なります。
特に標準偏差未満の値がまるで違うのです。
標準偏差未満の値が約76.6%(理論値67.8%)
標準偏差2倍未満の値が約95.8%(理論値95.3%)
標準偏差3倍未満の値が98.4%(理論値99.7%)
結論から言えば、
日経平均の値動きは明らかに正規分布ではありません。
不思議なのは標準偏差2倍未満の合計値は正規分布にほぼ一致してるところですが、
その次の3倍未満ででまたズレが生じてます。
この結果、3倍未満の値の発生確率は98.4%になってしまいまいした。
理論値との差は1.3%、本来なら誤差の内(通常の統計では5%以内)なんですが、
この数字、現実の株式市場では大きな意味を持ちます。
理論値では、標準偏差の3倍幅を超える滅茶苦茶な大変動の発生確率は0.3%でした。
(正確には約0.28%)
それが実際の日経平均ではその5倍以上の確率、1.6%に跳ね上がっているわけです。
これが何を意味するか。
1年間を通じての株式市場が開かれるのは約245日ですから、
もし理論通りの約0.28%なら、一年ごとだと0.735日、つまり1日にもなりません。
すなわち規格外の暴騰暴落は、あっても年に1日か2日、うまく行けば
そんな日は無いまま1年が終わる可能性も高いのです。
ところが現実の日経平均における発生率は1.6%にもなります。
すなわち、現実の株式市場では、年に3.9日も
想定外と言っていい暴騰暴落が起きてる、という事です。
1年を通じて3回以上もそんな日があったら株式投資で破産するには十分でしょう。
要するに実際の株式市場は理論値で予測されるより、
はるかに大荒れする危険な乱数集団なのだ、という事です。
ただし単純に数値が大荒れする可能性が高い集団なのか、といえばそうでもなく、
落ち着いた変動率と言っていい標準偏差未満の数値もまた理論値より8.8%高い、76.6%にもなります。
この結果、標準偏差2倍未満の確率は19.2%で、理論値の27.5%に対し約7割に過ぎないのです。
同じく標準偏差3倍未満の確率は2.6%、理論値の約6割に過ぎません。
すなわちより多くの数値が標準偏差内の変動に集まる大人しい動きの集団でありながら、
同時に規格外の変動が5倍も多く発生する、という正規分布の乱数とはかなり異なる特徴を持ちます。
ちなみに、これを日経平均だけの特殊な例と思ったら、これまた大間違いで(笑)、
アメリカを代表する株式指数、ダウ工業平均で、同様に2008〜2016年、
約2000のデータを元に、同じように上昇率の分布を見たのが以下のグラフ。
ちなみにこちらは平均値100%、標準偏差1.28%となってます。
日経平均より少し狭い標準偏差、つまり値動きの幅となってますが、
とりあえずマッターホルン絶好調でニューヨークにも登場、という感じですね。
もう一目でわかると思いますが、これも正規分布にはなってません。
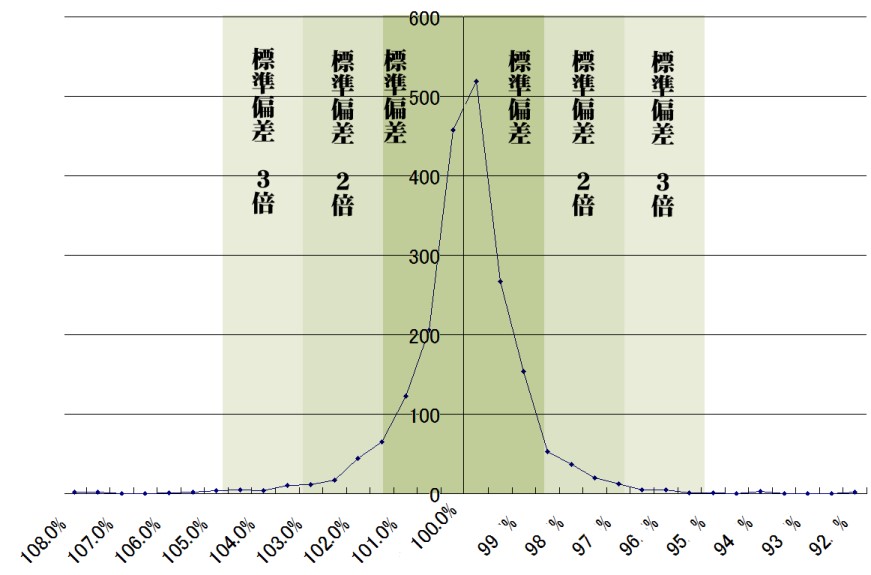
こちらも同じように含有量を確認して置くと、
標準偏差未満の値が約79.9%(理論値67.8%)
標準偏差2倍未満の値が約95.1%(理論値95.3%)
標準偏差3倍未満の値が98.3%(理論値99.7%)
と日経平均の分布と最大誤差3%前後でほぼ一致する、という数値になってます。
世界の株式市場は連動する傾向がある、とはいえ、
独立した市場の、全く異なる数字の指数の上昇率がここまで一致する以上、
なんらかの普遍性を持つ数字だと思っていいでしょう。
実は書いてる本人が、ここまで見事な展開になると全く予想してなかったので、
恐らく一番驚いてるのですが(笑)、どうも市場価格の上昇率による乱数集団は、
正規分布とは異なりながらも、一定の規格にそった分布を見せる、なにか別の乱数集団なのかもしれません。
それが何かと問われると現状全く判らないとしか言いようがないのですが。
とりあえず、今回の結論を書いておくと、以下の通りになります。
■株式市場における価格上昇率の乱数集団は正規分布ではない
■その乱数分布は複数の市場で普遍性がある
ここから導き出される当然の結論として、
金融工学において、市場が正規分布の乱数となる前提で組み立てられた理論は何の裏付けもない。
すなわちその正しさはほぼ世界的に保証されない。
という事になります。
乱数系の微積分でもっとも使われる伊東の補題はまさにこの前提に立ちますから、
それを取り込んだ理論は全部、前提条件が間違ってる可能性が高いよ、という話です。
まあ少なくとも、私は現代の金融工学の8割は茶番だ、と考える事にします。
といった辺りで、今年の話はここまで。
驚いた人は、それなりに驚いてくれた内容だったと思いますが(笑)、
実はまだこれでも、入り口に立っただけです。
ただしこの先の話は私自身も完全には解決して無いので、当面はここまでとします。
BACK