さて、次は重心と重心点について。
ヤジロベエや天秤といった日常的な装置で
重心とオモリの関係は確認が可能なので、重心がどういったものかは
皆さんよくご存知だと思います。
ただし、重心の定義をキチンとやろうとすると意外に難しいのですが、
とりあえずこの記事では、そこに力を加えると、物体全体に力を加えたのと
同じ効果が得られる点、としておきます。
それは一体、どういう意味?というのを説明しておきましょう。
今回の舞台は地球上です。
まず1kgのオモリを両脇につけた1mの棒を考えます。
両者を繋ぐ棒は極めて軽量なため、
その重さは無視できるとしましょう。
これを地面に置くと、当然、安定してそこに静止します。
図にするとこんな感じですね。

重力によってオモリが地面を押す力(作用)と
地面がこれを押し返す力(反作用)がつりあって
そこで安定してる、と考えられるわけです。
力(F)=質量(1kg)×重力加速度(9.86m/ss)ですから、
力の大きさは9.86kg m/ss×2個となっています。
ここで、この物体の重量に十分耐えうる支点でこれを支える、
という場合を考えてみましょう。
まずはこんな感じでバランス悪く行ってみます。
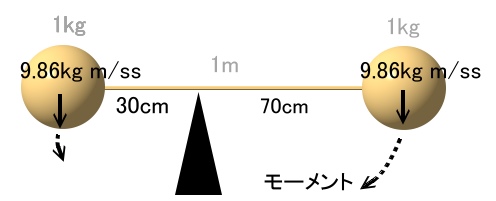
私たちは、経験上、これだと右下に傾く、というのを知っています。
右のほうが支点からの距離が長いからですね。
この支点からの距離と力の大きさの関係については
力(F)×支点までの距離(L)=回転の力・モーメント(N)
という式が成立します。
モーメント(略記号はN)は回転方向を持ったベクトルで、
物体が円運動する時の力の大きさと向きを示すものです。
エンジンやモーターの出力を意味するトルクと
基本的は同じ概念となります。
ただし上の式の証明と、モーメントの考え方を
キチンと説明しようとすると、
ベクトルの積という面倒な問題が出てくるので、
とりあえず、こういった式がある、というのだけを覚えておいてください。
ベクトルの向きは支点までの棒の長さを
半径とする円周となり、その大きさは上の式で求められるわけです。
で、この式から、物体を支える棒などは、
支点までの距離(L)が長い方が
回転の力のベクトル、モーメントが大きくなる、
すなわち生じる力が大きい、というのがわかります。
これはテコの原理そのものですね。
これによって同じ重さのものをテコで持ち上げる場合、
支点からより遠く離れた位置に力点を置くと、
より小さな力で持ち上げる事が可能なわけです。
なので、この図の場合も、同じ重さの物体ながら、
より長い70cmの位置にある
右のオモリの方がより強い回転の力を持つため、
棒を右下に傾ける、という事になります。
では、次に支点からの両者の距離を等しくします。
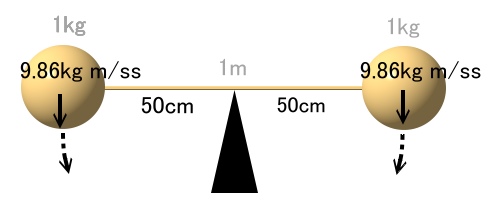
当然、吊り合いますね。
支点からの距離が同じなら、左右にかかる力が同じである以上、
これは慣性状態となって、その状態で静止する事になります。
この支点で支えたとき、左右の重さが吊り合う場所、
これが重心の基本的な位置となります。
その点で物体を支えると、回転しようとする力、モーメントが打ち消し合って
物体を慣性状態とする点、それが重心です。
ここで、一番上の上の図、この物体を
ゴロンと地面に転がした状態を思い出してください。
この時は物体全体が地面から力を受けて、
つまり全体で均等に力を受けて安定、静的安定の
慣性状態になっていたわけです。
そして支点で物体を支えるのは、これと同じ状態、
全体を静的安定、慣性状態に置くわけですから、
これは支点に対して力を加えると、
物体全体に同じ大きさの力を及ぼしたのと同じ効果を得られる、
という事を意味します。
さらに、これは静的安定状態に限りません。
例えば、この物体を押し上げる場合、地面ごと上に持ち上げても、
支点で支えて上に持ち上げても、
どちらでも左右のオモリは静止状態のまま、上に移動する事になります。
つまり、物体全体に、均一に力を加えるのと、
重心に対して力を加えるのとは、同じ結果となる、という事です。
だったら、力学的な作用は、物体の重心に働く、
と考えて計算してしまっても事実上問題が無い、
という事になるわけです。
この重心を重心点と呼び、運動の計算において
この点を対象とする事で、計算の簡易化を測るのが
ニュートン力学では普通に行なわれます。
これはとても重要な点なので、必ず覚えてください。
例えば地球のような巨大な物体でも、
あるいはジェット旅客機のような複雑な構造の物体でも、
その重心点に対して力は作用する、と考えると、計算がとても楽になるのです。
なので、夕撃旅団の記事においても、
基本的に物体全体の運動であり、重心点で話が済む場合は、
基本的に重心点に対する力のやり取りとして取り扱って行きます。

飛行中の機体にかかる重力、というのを考える場合、機首とエンジンと主翼と…
と全ての点にかかる重力とその作用と反作用を計算してたら、膨大な計算量になり、
容易には扱えないデータ量で溢れかえる事になります。
が、機体にかかる全重力が重心点にかかる、と考えても、
その結果が同じなら、圧倒的に簡単に同じ答えにたどり着く事ができるわけです。
ただし、航空機の場合、機体の重心と、主翼の揚力の重心がずれていたり、
飛行中に燃料タンクが空になってゆくにつれて
重心の位置が移動したりと、面倒な話がいろいろあるのですが、
それらはまた、別の記事で。
ちなみに、先に書いた力(F)×支点までの距離(L)の式により、
機体を上下左右に動かす尾翼は、可能な限り重心から遠い方が、
より小さな力で簡単に機体をコントロールできるようになる、というのが分かります。
ほとんどの航空機で、尾翼が一番後ろの位置にあるのはこのためです。
尾翼が重心に近づくに連れて、大きな力を産まないとならず、
そのため尾翼は大型化する必要があるわけで、
それは当然、無駄な重量増を招きます。
ついにで写真の重心点の位置は、凡そであり、適当です。
参考にはしないでください(笑)。


そのよい例を。
F-22への道でも指摘しましたが、機体の重心がヤケに後ろに片寄ってるF-22は
重心から尾翼までの距離が短く、その結果、水平、垂直両尾翼は
F-15に比べて、かなり大型のものになってます。
これだと重さはかさむわ、ステルスの敵、垂直尾翼は大型化するわで、
あまりほめられた設計ではない、と思うんですが、
プロの設計屋さんがこれを選んだんですから、何か理由があるんでしょうね…。
ちなみに、地球などの(ほぼ)球体では重心点は単純にその中心になります。
惑星の運動などは、基本的にこの重心点を基準に計算するわけです。
ただし、これが可能なのはあくまで物体全体に力がかかるのを
外部から観察する場合、だけです。
例えば、地球の周りを回る月など、独立した物体に
地球の引力が及ぼす影響は、地球と月の両者の重心点で考えて問題ありません。
が、剛体、つまり連続した物体として考えた地球の運動、例えば自転によって
地殻部分の受ける影響、といった問題では、この計算はできません。
ただ、夕撃旅団の記事で扱う内容で、
そこまで細かいものはほとんど無いと思うので、
とりあえずは、基本的に重心点で計算してゆく、と
考えておいてもらって大丈夫でしょう。
はい、今回はここまで。
これにてニュートン力学のお約束編は終了で、
あとは仕事とエネルギーと熱を残すのみでヤンス。
BACK