もう一つ、力&エネルギーの総和は常に一定である、というベルヌーイの定理を利用した
重要な部位が航空機にはあるので、せっかくなのでそちらも説明して置きましょう。

それがこのピトー管です。
写真のF-104だと機首先端部にビヨーンと延びてるものですね。
同じ流速で受ける全圧は常に一定の数字になる、というベルヌーイの法則を利用して、
静圧(気圧)と全圧の差から動圧と速度を求めるものです。

ちなみに単発のレシプロ機だと、主翼の端っこの方についてるのが多いです。
こちらはT-6テキサンで、どちらも浜松の航空自衛隊の広報館に展示中の機体。
その先端部には丁寧に防塵カバーが付いてます。
ホコリが入って穴が詰まってしまうと動かなくなるので、その用心ですが、
展示機ですから、本来は要らないはず。まあ、一種の演出でしょうね。
ついでに赤い札は、飛行前に必ず外せ、という警告です。
これを付けたままだと、ピトー管に空気が入らず、速度が全く判らなくなってしまいます。
速度が判らないと、離着陸の際に極めて危険ですから、要注意です。
でもって、そのピトー管で速度を知るための動作原理は以下の通り。
まあ、よく考えたな、という感じになってます。
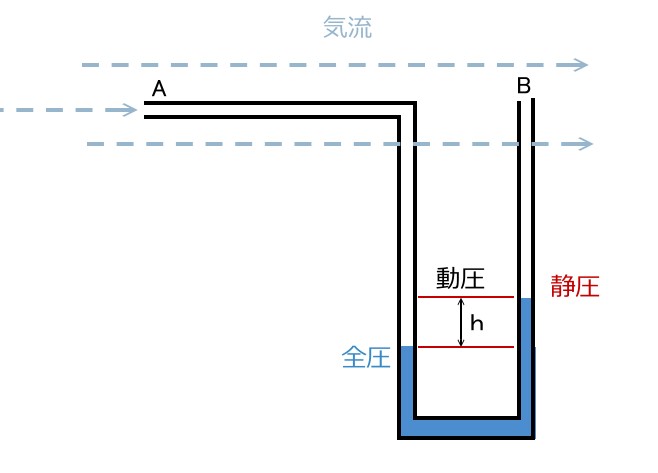
まず、パイプの底に液体を詰めます。
そのパイプの片方Aの口を流れに沿って(つまり機首の方向に)、
もう一方のBを流れと並行方向、つまり流れの影響を全く受けない垂直方向に開きます。
こうするとAの口は流体の持つ全圧、すなわち動圧+静圧を受けます。
対して流れに平行な方向を向くBの口は動圧を受けないので、
静圧、つまり大気圧のみを受けます。
当然、飛行中は静圧だけの方が力&エネルギーの値が低いので、
パイプの底の液体はAの側から押し下げられ、Bの口の側が高く上ります。
ここで、
全圧=動圧+静圧
よって
全圧 - 静圧 =動圧
ですから、パイプ内に発生する高低差 h は、B側に加わってない
動圧分の力だけで持ち上げられてた高さになります。
すでに何度も説明してるように、流体においては、力とエネルギーは同じ量ですから、
h の位置エネルギーの大きさは動圧の力の大きさに等しくなります。
よって、その位置エネルギーを求めれば
流速から受けている動圧の力がわかる事になるのです。
これは先ににベルヌーイの定理の所で見たように、
位置エネルギー = 密度×重力加速度×高さ
ですから
位置エネルギー= 液体の密度 × 重力加速度 × h の高さ
で求める事が可能です。
自分で入れた液体である以上、液体の密度は判ってるとすると(笑)、
重力加速度9.8m/ssは高度3万メートルくらいまではほぼ不変ですから
後はhの高さが判れば、この流れの動圧が出ます。
でもって動圧は、
動圧(運動エネルギー)=1/2×密度×流速×流速
で求められました。今回の場合、密度は大気密度です。
で、これを流速を求める式に変換すると、
流速の二乗を残して全てを反対の辺に移動し、最後にルートを付けてやればいいので、
流速=√2×動圧÷大気密度
(*ルートは式全体にかかってます)
少し物理の数式っぽくすると、
v=√2×動圧/ρ
(*ルートは式全体にかかってます)
という計算式になります。で、動圧は既に先の位置エネルギーの計算で求めてあり、
大気密度は高度と温度が判れば推測できますから、
これにて機体の速度が判る、という事になります。
つまり管内に入れた液体の密度と、飛行時の高低差、h の値が判れば、
その時の飛行速度が求められることになるわけです。
これがピトー管の基本的な動作原理です。

再びF-104のピトー管の写真を。
手前の防塵カバーの中に前方の穴があり、
よく見るとその後ろに横向きの静圧測定用の穴があるのが判るかと。
こんな写真、撮ってどうすると思ってたんですが、意外に使うもんだなあ(笑)…
ただし高度によって温度が変る以上、中の液体の密度も変わってしまうので、
原理的にどうしても誤差が避けれません。
さらに大気密度も温度で変わって来ます。
その上、ピトー管がキチンと進行方向を向いてない状態、つまり迎え角がある状態だと、
管内の全圧は必ずしも動圧を完全に含んでません。
これらの事もあって、ピトー管とつながった計器で読み取れる速度は
常に誤差を含んでいるのが普通です。
なのでこれを指示対気速度(IAS)と呼んで、実際の速度、
真対気速度(TAS)と区別しています。
といった感じで、エネルギーと力が一緒、という流体力学の特徴から導き出される保存則、
ベルヌーイの定理と、そこから出てくる航空機に関わる現象を解説しました。
とりあえず、今回はここまで。
次回は、粘度を無視できない流体の話をやります。
BACK